题目内容
6.根据以上规律解答下题:若有理数a、b满足|a-1|+(b-3)2=0,试求:$\frac{1}{ab}$+$\frac{1}{(a+2)(b+2)}$+$\frac{1}{(a+4)(b+4)}$+…+$\frac{1}{(a+100)(b+100)}$的值.分析 根据非负数的性质列方程求出a、b的值,然后代入代数式再裂项进行计算即可得解.
解答 解:由题意得,a-1=0,b-3=0,
解得a=1,b=3,
所以,$\frac{1}{ab}$+$\frac{1}{(a+2)(b+2)}$+$\frac{1}{(a+4)(b+4)}$+…+$\frac{1}{(a+100)(b+100)}$,
=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{101×103}$,
=2×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{101}$-$\frac{1}{103}$),
=2×(1-$\frac{1}{103}$),
=$\frac{204}{103}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0,本题难点在于裂项.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
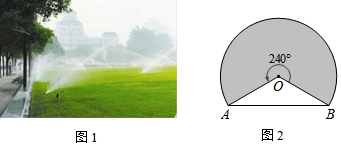
16.如图(1)是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是如图(2)所示的扇形.如果A,B两点的距离为18m,那么这种装置能够喷灌的草坪面积为72πm2.

17.若直角三角形两边长分别是6,8,则它的斜边为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 以上都不正确 |
4.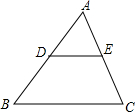 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
 如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )
如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
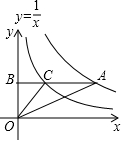 如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.
如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.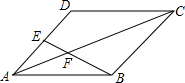 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F.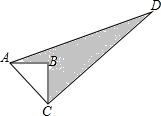 如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.
如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.