题目内容
6.在△ABC中,∠ACB=90°,a、b、c分别为∠A、∠B、∠C的对边,△ABC的面积为24,a+b=14,求c的长.分析 根据三角形的面积和a+b=14利用完全平方公式求出ab的值,再根据勾股定理求出c的值即可.
解答  解:如图:∵△ABC的面积为24,
解:如图:∵△ABC的面积为24,
∴$\frac{1}{2}$ab=24,
即ab=48,
∵a+b=14,
∴(a+b)2=142,
即a2+b2+2ab=196,
∴a2+b2+2×48=196,
∴a2+b2=100,
∴c=$\sqrt{100}$=10.
点评 本题考查的是勾股定理和三角形的面积公式,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
11.某私家车每次加油都把油箱加满,如表记录了该车相邻两次加油时的情况
注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每100千米平均耗油量为( )
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2016年2月8日 | 12 | 35000 |
| 2016年2月12日 | 48 | 35600 |
| A. | 6升 | B. | 10升 | C. | 8升 | D. | 12升 |
15.已知锐角三角形的两边长分别3、4,则第三边长x的取值范围是( )
| A. | 1<x<7 | B. | 1<x<5 | C. | $\sqrt{7}$<x<5 | D. | 1<x<$\sqrt{7}$ |
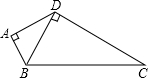 如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.
如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2. 如图,一次函数y1=ax+b的图象与反比例 函数y2=$\frac{k}{x}$的图象交于M,N两点.
如图,一次函数y1=ax+b的图象与反比例 函数y2=$\frac{k}{x}$的图象交于M,N两点.