题目内容
14.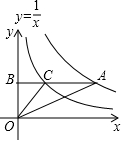 如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.
如图,在直角坐标系中,Rt△OAB的边在y轴上,∠ABO=90°,∠BOC=∠A=30°,双曲线y=$\frac{1}{x}$经过点C,双曲线y=$\frac{k}{x}$经过点A,则k的值为3.
分析 设C(a,b),根据直角三角形的性质和等腰三角形的性质求得A(3a,b),根据反比例函数图象上点的在特征k=xy,即可求得结果.
解答 解:∵∠ABO=90°,
∴AB∥x轴,
∵∠ABO=90°,∠BOC=∠A=30°,
∴OC=2BC,∠AOB=60°,
∴∠AOC=30°,
∴∠AOC=∠A,
∴OC=AC,
设C(a,b),
∴OC=2a,
∴AB=3a,
∴A(3a,b),
∵曲线y=$\frac{1}{x}$经过点C,
∴ab=1,
∵双曲线y=$\frac{k}{x}$经过点A,
∴k=3a•b=3.
故答案为3.
点评 本题考查了反比例函数图象上点的坐标特征,直角三角形的性质以及等腰三角形的性质,熟练掌握反比例函数y=$\frac{k}{x}$中,k=xy是解题的关键.

练习册系列答案
相关题目
19.如果不等式组$\left\{\begin{array}{l}{-1<x≤3}\\{x>m}\end{array}\right.$ 有解,那么m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<-1 | D. | -1<m<3 |
11.某私家车每次加油都把油箱加满,如表记录了该车相邻两次加油时的情况
注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每100千米平均耗油量为( )
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2016年2月8日 | 12 | 35000 |
| 2016年2月12日 | 48 | 35600 |
| A. | 6升 | B. | 10升 | C. | 8升 | D. | 12升 |
 如图,在四边形ABCD中,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为36.
如图,在四边形ABCD中,已知AB=4,BC=3,AD=12,DC=13,∠B=90°,则四边形ABCD的面积为36.