题目内容
16.如图(1)是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是如图(2)所示的扇形.如果A,B两点的距离为18m,那么这种装置能够喷灌的草坪面积为72πm2.
分析 作OC⊥AB,根据垂径定理得出AC=9,继而可得圆的半径OA的值,再根据扇形面积公式可得答案.
解答 解:过点O作OC⊥AB于C点.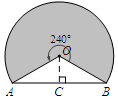
∵OC⊥AB,AB=18,
∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$×18=9(cm),
∵OA=OB,∠AOB=360°-240°=120°,
∴∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×120=60°.
在Rt△OAC中,OA2=OC2+AC2,
又∵OC=$\frac{1}{2}$OA,
∴r=OA=6$\sqrt{3}$.
∴S=$\frac{240}{360}$πr2=72π(m2).
故答案是:72π.
点评 本题主要考查垂径定理和扇形的面积公式,熟练掌握垂径定理求得圆的半径是解题的关键.

练习册系列答案
相关题目
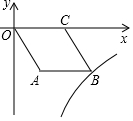 如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(6,-8),顶点C在x轴的正半轴上,若函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )