题目内容
已知实数a、b分别满足3a4+2a2-4=0和b4+b2-3=0,则4a-4+b4= .
考点:根与系数的关系,实数的运算
专题:计算题
分析:先由求根公式求出a2和b2的值,再代入4a-4+b4,进行化简即可.
解答:解:3a4+2a2-4=0,
∴a2=
=
,
∵a2≥0,
∴a2=
;
同理由b4+b2-3=0,求出b2=
;
4a-4+b4=
+(b2)2
=
+(
)2
=
+
=
+
=
+
=7.
故答案为:7.
∴a2=
-2±
| ||
| 2×3 |
-1±
| ||
| 3 |
∵a2≥0,
∴a2=
-1+
| ||
| 3 |
同理由b4+b2-3=0,求出b2=
-1+
| ||
| 2 |
4a-4+b4=
| 4 |
| (a2)2 |
=
| 4 | ||||
(
|
-1+
| ||
| 2 |
=
| 18 | ||
7-
|
7-
| ||
| 2 |
=
18×(7+
| ||||
(7-
|
7-
| ||
| 2 |
=
7+
| ||
| 2 |
7-
| ||
| 2 |
=7.
故答案为:7.
点评:本题主要考查了求根公式和实数的运算的应用,主要考查学生的计算能力,题目较好,但有一定的难度.

练习册系列答案
相关题目
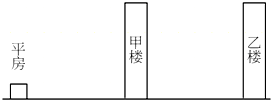 窗台高1.2米,该地区冬天中午12时阳光从正南方照射时,光线与水平线的最小夹角为30°.
窗台高1.2米,该地区冬天中午12时阳光从正南方照射时,光线与水平线的最小夹角为30°.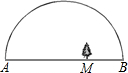 方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米.
方案设计:儿童公园有一块半圆形空地,如图11所示,根据需要欲在此半圆内划出一个三角形区域作为健身场地,其中内接于此三角形的矩形区域为儿童游乐场,已知半圆的直径AB=100米,若使三角形的顶点C在半圆上,且AC=80米. 图中所示为“三角城”的街道图.若某人欲从O点走到B点,但只能沿着街道向东、北或东北走,则共有
图中所示为“三角城”的街道图.若某人欲从O点走到B点,但只能沿着街道向东、北或东北走,则共有