题目内容
图中所示为“三角城”的街道图．若某人欲从O点走到B点，但只能沿着街道向东、北或东北走，则共有考点：计数方法
专题：规律型
分析：先根据图形数出有多少个三角形，在根据三角形的边数得出1个三角形的不同走法，再根据1，2，3层的三角，即可求出答案．
解答：解：根据题意得：
图中有14个三角形，每个三角形有三条边，
所以1个三角形就有14×3=42种不同的走法，
再根据最低层有7个三角形，第二层有2个，第三层3个，第四层1个，再加上外边1个大的，
即7×2×3×1+1=43，
所以共有：42×43=1806（种）．
故答案为：1806．
图中有14个三角形，每个三角形有三条边，
所以1个三角形就有14×3=42种不同的走法，
再根据最低层有7个三角形，第二层有2个，第三层3个，第四层1个，再加上外边1个大的，
即7×2×3×1+1=43，
所以共有：42×43=1806（种）．
故答案为：1806．
点评：此题考查了计算法；解题的关键是找出图中的三角形，再结合三角形的边数，通过观察得到走法的规律．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
圆锥形的烟囱冒的底面直径是80cm，母线长是50cm，制作100个这样的烟囱冒至少需要
如图，四边形ABCD为某一住宅区的平面示意图，其周长为800m，为了美化环境，计划在住宅区周围5m内（虚线以内，四边形ABCD之外）作为绿化带，则绿化带的面积为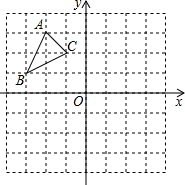
如图，△ABC中A（-2，3），B（-3，1），C（-1，2）．