题目内容
6.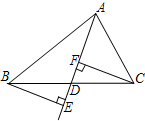 如图,AD是△ABC的中线,BE⊥AD,CF⊥AD,垂足分别为E,F,求证:AE+AF=2AD.
如图,AD是△ABC的中线,BE⊥AD,CF⊥AD,垂足分别为E,F,求证:AE+AF=2AD.
分析 由条件可证明△BED≌△CFD,再利用线段和差可证得结论.
解答 证明:
∵AD是△ABC的中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD,
在△BED和△CFD中
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠BDE=∠CDF}\\{BD=CD}\end{array}\right.$
∴△BED≌△CFD(AAS),
∴DE=DF,
∴EF=2DF,
∴AE+AF=AF+EF+AF=2AF+2DF=2(AF+DF)=2AD.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等,对应角相等)是解题的关键.

练习册系列答案
相关题目
16. 如图所示,在A处观察C,得仰角∠CAD=31°,且A、B的水平距离AE=800米,AB的坡度i=1:2,索道BC的坡度i=2:3,CD⊥AD于D,BF⊥CD于F.则索道BC的长大约是( )(参考数据:tan31°≈0.6,cos31°≈0.9,$\sqrt{13}$≈3.6)
如图所示,在A处观察C,得仰角∠CAD=31°,且A、B的水平距离AE=800米,AB的坡度i=1:2,索道BC的坡度i=2:3,CD⊥AD于D,BF⊥CD于F.则索道BC的长大约是( )(参考数据:tan31°≈0.6,cos31°≈0.9,$\sqrt{13}$≈3.6)
 如图所示,在A处观察C,得仰角∠CAD=31°,且A、B的水平距离AE=800米,AB的坡度i=1:2,索道BC的坡度i=2:3,CD⊥AD于D,BF⊥CD于F.则索道BC的长大约是( )(参考数据:tan31°≈0.6,cos31°≈0.9,$\sqrt{13}$≈3.6)
如图所示,在A处观察C,得仰角∠CAD=31°,且A、B的水平距离AE=800米,AB的坡度i=1:2,索道BC的坡度i=2:3,CD⊥AD于D,BF⊥CD于F.则索道BC的长大约是( )(参考数据:tan31°≈0.6,cos31°≈0.9,$\sqrt{13}$≈3.6)| A. | 1400 | B. | 1440 | C. | 1500 | D. | 1540 |
1. 如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
 如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论:
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论: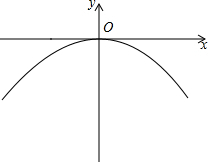 有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m.
有一座抛物线形拱桥,正常水位时,桥下水面宽20m,拱顶距离水面4m. 如图是2015年11月的日历.
如图是2015年11月的日历.