题目内容
14. 如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论:
如图,AB为⊙O的直径,AC交⊙O于E点,BC交⊙O于D点,CD=BD,∠C=70°,现给出以下四个结论:①∠A=40°;
②AC=AB;
③$\widehat{AE}$=$\widehat{BE}$;
④2CE•AB=BC2,
其中正确结论的序号为①②④.
分析 ①②正确,只要证明△ABC是等腰三角形即可;③错误.假设成立,推出矛盾即可;④正确,只要证明△CED∽△CBA即可.
解答 解:连接AD、BE、ED.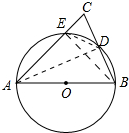
∵AB是直径,
∴∠ADB=90°,即AD⊥BC,
∵DC=DB,
∴AC=AB,故②正确,
∴∠C=∠ABC=70°,
∴∠BAC=180°-∠C-∠ABC=40°,故①正确,
∵∠C=∠C,∠CED=∠ABC,
∴△CED∽△CBA,
∴$\frac{CE}{CB}$=$\frac{CD}{CA}$,
∴CE•CA=CB•CD,
∵AB=AC,CD=$\frac{1}{2}$BC,
∴CE•AB=BC•$\frac{1}{2}$BC,
∴2CE•AB=BC2,故④正确,
不妨设③成立,则,∠EAB=∠EBA=45°,与已知条件矛盾,
∴假设错误,故③错误,
故答案为①②④
点评 本题考查圆的有关知识、相似三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是熟练掌握这些知识的应用,学会添加常用辅助线,学会把证明等积式,转化为证明三角形相似,属于中考常考题型.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
19. 将正整数按如图所示的位置顺序排列:
将正整数按如图所示的位置顺序排列:
根据排列规律,则2016应在( )
 将正整数按如图所示的位置顺序排列:
将正整数按如图所示的位置顺序排列:根据排列规律,则2016应在( )
| A. | A处 | B. | B处 | C. | C处 | D. | D处 |
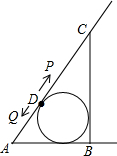 如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.
如图,△ABC中,CB=8,AB=6,AC=10,△ABC的内切圆交 AC于点D,点P从D出发,沿射线DC每次前进一个单位,点Q从D出发沿DA和射线AB每次前进a个单位,a为正整数且1≤a<5,当t次前进后△APQ与△ABC相似,所有满足条件的t为8、16、32.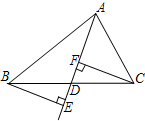 如图,AD是△ABC的中线,BE⊥AD,CF⊥AD,垂足分别为E,F,求证:AE+AF=2AD.
如图,AD是△ABC的中线,BE⊥AD,CF⊥AD,垂足分别为E,F,求证:AE+AF=2AD.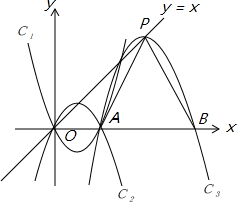 已知抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2.
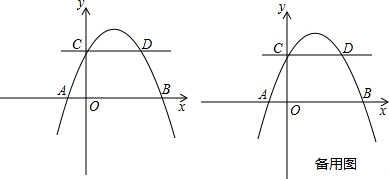
已知抛物线C1的解析式为y=(x-1)2-1,将C1沿x轴翻折得抛物线C2.