题目内容
1. 如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )
如图,将周长为12的△DEF沿FE方向平移1个单位得到△ABC,则四边形ABFD的周长为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 根据平移的基本性质,得出四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC即可得出答案.
解答 解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=12,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=14.
故选:C
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.得到CF=AD,DF=AC是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
16. 如图,圆的周长为4个单位.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2015的点与圆周上表示数字( )的点重合.
如图,圆的周长为4个单位.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2015的点与圆周上表示数字( )的点重合.
 如图,圆的周长为4个单位.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2015的点与圆周上表示数字( )的点重合.
如图,圆的周长为4个单位.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2015的点与圆周上表示数字( )的点重合.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.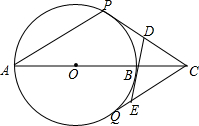 如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
 如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )
如图,AB是⊙O的直径,点C是AB延长线上一点,且OB=BC,CP、CQ、DE是⊙O的切线,P、Q是切点,若⊙O的半径为2,则△CDE的周长为( )| A. | 4 | B. | 6 | C. | 4$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
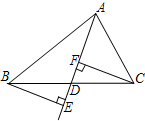 如图,AD是△ABC的中线,BE⊥AD,CF⊥AD,垂足分别为E,F,求证:AE+AF=2AD.
如图,AD是△ABC的中线,BE⊥AD,CF⊥AD,垂足分别为E,F,求证:AE+AF=2AD.