题目内容
4．已知方程x2+（m-1）x+m-10=0的一个根是3，则m的值是1．分析 将x=3代入方程x2+（m-1）x+m-10=0，得到关于m的一元一次方程，解方程即可求得m的值．
解答 解：∵方程x2+（m-1）x+m-10=0的一个根是3，
∴9+3（m-1）+m-10=0，
即4m-4=0，
解得m=1．
故答案为1．
点评 本题考查的是一元二次方程的解（根）的意义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．也考查了一元一次方程的解法．
练习册系列答案
名校课堂系列答案
相关题目
14．
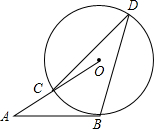如图，AB是⊙O的切线，切点为B，AO交⊙O于点C，D是优弧BC上一点，∠A=30°，则∠D为（ ）
如图，AB是⊙O的切线，切点为B，AO交⊙O于点C，D是优弧BC上一点，∠A=30°，则∠D为（ ）| A． | 25° | B． | 30° | C． | 35° | D． | 45° |
12．
如图，将矩形ABCD沿DE折叠，点A恰好落在BC上的点F处，点G、H分别在AD、AB上，且FG⊥DH，若tan∠ADE=$\frac{1}{2}$，则$\frac{GF}{DH}$的值为（ ）
如图，将矩形ABCD沿DE折叠，点A恰好落在BC上的点F处，点G、H分别在AD、AB上，且FG⊥DH，若tan∠ADE=$\frac{1}{2}$，则$\frac{GF}{DH}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{3}{5}$ |
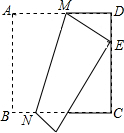如图，将边长为12cm的正方形纸片ABCD折叠，使得点A落在边CD上的E点，折痕为MN，若MN的长为13cm，则CE的长为7cm．
16．若m=$\sqrt{40}$-5，则估计m的值所在的范围是（ ）
| A． | 1＜m＜2 | B． | 2＜m＜3 | C． | 3＜m＜4 | D． | 4＜m＜5 |
直线a∥b，一块含30°角的直角三角板如图放置，∠1=24°，则∠2为36°．