题目内容

12．如图，?ABCD的面积为72cm2，P为?ABCD内部的任意一点，则图中阴影部分的面积之和为36cm2．

分析 过点P作EF∥AD，GH∥AB得到四边形AEPG、四边形EPHB，四边形GPFD、四边形PFCH均为平行四边形，从而得到阴影部分的面积为平行四边形的面积的一半．

解答 解：如图，过点P作EF∥AD，GH∥AB，
则四边形AEPG、四边形EPHB，四边形GPFD、四边形PFCH均为平行四边形，
在平行四边形AEPG中，
∵AP是对角线，
∴S△AEP=S△APG，
∴阴影部分的面积为平行四边形的面积的一半，即36cm2．
故答案为：36cm2．

点评 本题考查了平行四边形的性质，解题的关键是构造平行四边形并利用平行四边形的对角线平分平行四边形的面积求解．

练习册系列答案
相关题目
2．计算：
（1）（x-1）（x+1）=x2-1；
（2）（x-1）（x2+x+1）=x3-1；
（3）（x-1）（x3+x2+x+1）=x4-1；
由此我们可以得到（x-1）（x99+x98+…+x+1）=x100-1；
请你利用上面的结论，完成下面两题的计算：
（1）299+298+…+2+1；      
（2）（-3）50+（-3）49+…+（-3）+1．
3．下列各式一定是二次根式的是（　　）
A．$\sqrt{-7}$B．$\sqrt{x}$C．$\sqrt{{x^2}+{y^2}}$D．$\root{3}{6}$
20．农机厂职工到距工厂15千米的某地检修农机，一部分人骑自行车先走40分钟后，其余人乘汽车出发，结果他们同时到达．已知汽车速度为自行车速度的3倍，若设自行车的速度为x千米/时，则所列方程为$\frac{15}{3x}$=$\frac{15}{x}$-$\frac{40}{60}$．
7．下列运算正确的正确的是（　　）
A．$\sqrt{2m}$+$\sqrt{3m}$=$\sqrt{5m}$B．5$\sqrt{5}$-$\sqrt{5}$=4C．5+$\sqrt{2}$=5$\sqrt{2}$D．m$\sqrt{x}$-n$\sqrt{x}$=（m-n）$\sqrt{x}$
17．在进行二次根式计算或化简时，我们有时会碰上如$\sqrt{5+2\sqrt{6}}$这种“双重根式”，同学们总觉得已不能进一步化简和计算；其实我们还可以利用a=（$\sqrt{a}$）2（a≥0）和$\sqrt{{a}^{2}}$=|a|这两个二次根式的性质进行化简，其解决办法是拆“项”配方，见下面化简过程：
$\sqrt{5+2\sqrt{6}}$=$\sqrt{3+2\sqrt{6}+2}$=$\sqrt{（\sqrt{3}）^{2}+2\sqrt{6}+（\sqrt{2}）^{2}}$=$\sqrt{（\sqrt{3}+\sqrt{2}）^{2}}$=$\sqrt{3}$+$\sqrt{2}$
根据上面的解法，请计算：
（1）$\sqrt{7-4\sqrt{3}}$；            
（2）$\frac{2}{\sqrt{2}}$-（$\sqrt{3}$-2）2014（$\sqrt{3}$+2）2015+$\sqrt{3-2\sqrt{2}}$-|$\sqrt{3}$-2|
4．⊙O1的半径为3厘米，⊙O2的半径为2厘米，圆心距O1O2=4厘米，这两圆的位置关系是（　　）
A．内含B．内切C．相交D．外切
1．在下列二次根式中，x的取值范围是x＞3的是（　　）
A．$\sqrt{3-x}$B．$\sqrt{x+3}$C．$\sqrt{x-3}$D．$\sqrt{\frac{1}{x-3}}$
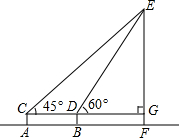2．如图，为了测得铁塔的高度，小莹利用自制的测角仪，在C点测得塔顶E的仰角为45°，在D点测得塔顶E的仰角为60°，已知测角仪AC的高为1.6米，CD的长为6米，CD所在的水平线CG⊥EF于点G，铁塔EF的高为（10.6+3$\sqrt{3}$）米．（结果用带根号的式子表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网