题目内容
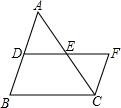 如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10,
如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10,BC=8,求四边形BCFD的周长.
考点:全等三角形的判定与性质,平行四边形的判定与性质
专题:
分析:根据D、E分别是AB、AC的中点,可得DE∥BC,DF=
BC,再由EF=DE,得EF=
BC,DE+EF=DF=BC,从而得出四边形BCFD是平行四边形;进一步求得周长即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵D、E分别是AB、AC的中点,
∴DE∥BC,DE=
BC,
∵EF=DE,
∴EF=
BC,
∴DE+EF=DF=BC,
∴四边形BCFD是平行四边形.
四边形BCFD的周长=(5+8)×2=26.
∴DE∥BC,DE=
| 1 |
| 2 |
∵EF=DE,
∴EF=
| 1 |
| 2 |
∴DE+EF=DF=BC,
∴四边形BCFD是平行四边形.
四边形BCFD的周长=(5+8)×2=26.
点评:本题考查了平行四边形的判定,解题的关键是牢记平行四边形的判定定理是解决问题的关键.

练习册系列答案
相关题目
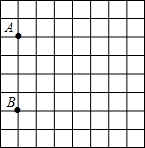 有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长.
有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长. 如图,AB=EB,BC=BF,∠ABE=∠CBF.求证:EF=AC.
如图,AB=EB,BC=BF,∠ABE=∠CBF.求证:EF=AC.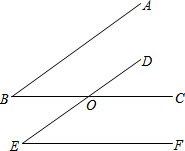 已知如图BC交DE于O,给出下面三个论断:
已知如图BC交DE于O,给出下面三个论断: 如图,在10×6的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移5个单位,得到△A′B′C′,再把△A′B′C′绕点A′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法).
如图,在10×6的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移5个单位,得到△A′B′C′,再把△A′B′C′绕点A′顺时针旋转90°,得到△A″B″C″,请你画出△A′B′C′和△A″B″C″(不要求写画法). 如图,△ABC中,AD是高,AE平分∠BAD,∠B=20°,则∠EAD=
如图,△ABC中,AD是高,AE平分∠BAD,∠B=20°,则∠EAD=