题目内容
已知二次函数y=x2-x-6.
(1)求该抛物线与x轴的交点坐标及顶点坐标;
(2)画出图象;
(3)观察图象,指出方程x2-x-6=0的解及使不等式x2-x-6<0成立的取值;
(4)求抛物线与坐标轴所构成的三角形面积.
(1)求该抛物线与x轴的交点坐标及顶点坐标;
(2)画出图象;
(3)观察图象,指出方程x2-x-6=0的解及使不等式x2-x-6<0成立的取值;
(4)求抛物线与坐标轴所构成的三角形面积.
考点:抛物线与x轴的交点,二次函数的图象,二次函数的性质,二次函数图象上点的坐标特征,二次函数与不等式(组)
专题:
分析:(1)抛物线与x轴交点的纵坐标等于零;将二次函数解析式转化为顶点式方程,根据解析式写出顶点坐标;
(2)由抛物线开口方向,与x轴交点坐标,顶点坐标画出图象;
(3)根据图象直接写出答案;
(4)由三角形的面积公式进行解答.
(2)由抛物线开口方向,与x轴交点坐标,顶点坐标画出图象;
(3)根据图象直接写出答案;
(4)由三角形的面积公式进行解答.
解答:解:(1)令y=0,则x2-x-6=0,
即:(x-3)(x+2)=0,
解得 x1=3,x2=-2,
故抛物线与x轴的交点坐标是(3,0),(-2,0).
∵y=x2-x-6=(x-
)2-
,
∴该抛物线的顶点坐标是(
,-
);
(2)由抛物线解析式y=x2-x-6知,该抛物线开口方向向上,且与y轴的交点是(0,-6).
由(1)知,抛物线与x轴的交点坐标是(3,0),(-2,0),顶点坐标是(
,-
).
则其图象如图所示:
 ;
;
(3)根据图象知,方程x2-x-6=0的解是x1=3,x2=-2;
不等式x2-x-6<0成立的x取值范围是:-2<x<3;
(4)如图所示:抛物线与坐标轴所构成的三角形面积是:
×|-2-3|×|-6|=15.即抛物线与坐标轴所构成的三角形面积是15.
即:(x-3)(x+2)=0,
解得 x1=3,x2=-2,
故抛物线与x轴的交点坐标是(3,0),(-2,0).
∵y=x2-x-6=(x-
| 1 |
| 2 |
| 25 |
| 4 |
∴该抛物线的顶点坐标是(
| 1 |
| 2 |
| 25 |
| 4 |
(2)由抛物线解析式y=x2-x-6知,该抛物线开口方向向上,且与y轴的交点是(0,-6).
由(1)知,抛物线与x轴的交点坐标是(3,0),(-2,0),顶点坐标是(
| 1 |
| 2 |
| 25 |
| 4 |
则其图象如图所示:
 ;
;(3)根据图象知,方程x2-x-6=0的解是x1=3,x2=-2;
不等式x2-x-6<0成立的x取值范围是:-2<x<3;
(4)如图所示:抛物线与坐标轴所构成的三角形面积是:
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点,二次函数的图象与性质等知识点.解题时,一定要数形结合.

练习册系列答案
相关题目
 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4). 已知:a、b、c为正实数,抛物线y=x2-2ax+b2与x轴交于M、N两点,交y轴于P点其中M的坐标(a+c,0).
已知:a、b、c为正实数,抛物线y=x2-2ax+b2与x轴交于M、N两点,交y轴于P点其中M的坐标(a+c,0).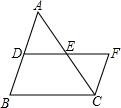 如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10,
如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10, 如图,正方形ABCD中,AC为对角线,E、F分别是边AB、AD上的两点,且CE=CF.求证:AE=AF.
如图,正方形ABCD中,AC为对角线,E、F分别是边AB、AD上的两点,且CE=CF.求证:AE=AF. 如图,已知∠α和∠β.
如图,已知∠α和∠β. 超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.一次性购物满300元者,如果不摇奖可返还现金15元.
超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.一次性购物满300元者,如果不摇奖可返还现金15元. 边形EFGH用围栏圈起来,划为保护区,请你计算保护区的周长和面积.
边形EFGH用围栏圈起来,划为保护区,请你计算保护区的周长和面积.