题目内容
 如图,AB=EB,BC=BF,∠ABE=∠CBF.求证:EF=AC.
如图,AB=EB,BC=BF,∠ABE=∠CBF.求证:EF=AC.考点:全等三角形的判定与性质
专题:证明题
分析:由已知角相等,利用等式的性质得到夹角相等,利用SAS得到三角形ABC与三角形EBF全等,利用全等三角形的对应边相等即可得证.
解答:证明:∵∠ABE=∠CBF,
∴∠ABE+∠ECB=∠CBF+∠ECB,即∠ABC=∠EBF,
在△ABC和△EBF中,
,
∴△ABC≌△EBF(SAS),
则EF=AC.
∴∠ABE+∠ECB=∠CBF+∠ECB,即∠ABC=∠EBF,
在△ABC和△EBF中,
|
∴△ABC≌△EBF(SAS),
则EF=AC.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,在菱形ABCD中,AD=13,BD=24,AC,BD交于点O.
如图,在菱形ABCD中,AD=13,BD=24,AC,BD交于点O. 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4).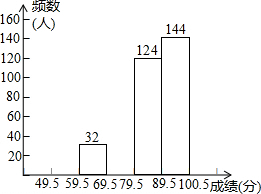 某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题:
某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题: 已知:a、b、c为正实数,抛物线y=x2-2ax+b2与x轴交于M、N两点,交y轴于P点其中M的坐标(a+c,0).
已知:a、b、c为正实数,抛物线y=x2-2ax+b2与x轴交于M、N两点,交y轴于P点其中M的坐标(a+c,0).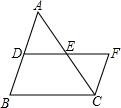 如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10,
如图,在△ABC中,D、E分别为AB、AC的中点,延长DE到F,使EF=DE,若AB=10, 边形EFGH用围栏圈起来,划为保护区,请你计算保护区的周长和面积.
边形EFGH用围栏圈起来,划为保护区,请你计算保护区的周长和面积.