题目内容
16.分式$\frac{1}{a+b}$,$\frac{2a}{{a}^{2}-{b}^{2}}$,$\frac{b}{b-a}$的最简公分母为( )| A. | (a2-b2)(a+b)(b-a) | B. | (a2-b2)(a+b) | C. | (a2-b2)(b-a) | D. | a2-b2 |
分析 确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
解答 解:分式$\frac{1}{a+b}$,$\frac{2a}{{a}^{2}-{b}^{2}}$,$\frac{b}{b-a}$的分母分别是a+b、a2-b2=(a+b)(a-b),b-a=-(a-b),故最简公分母是a2-b2;
故选D.
点评 本题考查了最简公分母的定义及求法,通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.一般方法:①如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数,相同字母的最高次幂,所有不同字母都写在积里.②如果各分母都是多项式,就可以将各个分母因式分解,取各分母数字系数的最小公倍数,凡出现的字母(或含字母的整式)为底数的幂的因式都要取最高次幂.

练习册系列答案
相关题目
11.a14可以写成( )
| A. | a7+a7 | B. | a7•a7 | C. | a5•a8 | D. | a8•a2 |
1.已知二次函数y=x2+4x+a,下列说法正确的是( )
| A. | 当x<1时,y随x的增大而减小 | |
| B. | 若图象与x轴有交点,则a≤4 | |
| C. | 当a=3时,不等式x2+4x+a>0的解集是1<x<3 | |
| D. | 若将图象向上平移1个单位,再向左平移3个单位后过点(1,-2),则a=-3 |
8.某家具厂销售1套A种款式和2套B种款式的家具的利润为1400元,销售2套A种款式和3套B种款式家具的利润为2400元
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
设甲种板材全部用完时恰好生产A款家具x套,两种款式家具全部售完时的销售利润为y元.
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
(1)求每套A种款式和每套B种款式家具的销售利润;
(2)该家具厂计划用甲种板材200m2,乙种板材250m2生产A、B两种款式的家具,每套所需板材情况如表:
| 甲种板材(m2) | 乙种板材(m2) | |
| A款 | 3 | 6 |
| B款 | 5 | 4 |
①求y与x之间的函数关系式;
②用这些板材生产的A、B两款家具,最大销售利润是多少?
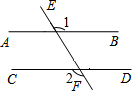 如图,直线AB,CD被EF所截,且AB∥CD,若∠1=126°,则∠2=126°.
如图,直线AB,CD被EF所截,且AB∥CD,若∠1=126°,则∠2=126°.