题目内容
5.关于x的不等式组$\left\{\begin{array}{l}{2(x-1)-3(x+2)>-6}\\{\frac{x+a}{2}>1}\end{array}\right.$恰有2个整数解,则a的取值范围为a>6.分析 求出不等式组的解集,得到其取值范围,再根据一元二次方程有整数解解答.
解答 解:$\left\{\begin{array}{l}2(x-1)-3(x+2)>-6①\\ \frac{x+a}{2}>1②\end{array}\right.$,
由①得,x<-2;
由②得,x>2-a;
∵恰有2个整数解,
∴2-a<x<-2;
∴整数解为-3,-4,
∴2-a<-4,
∴-a<-6,
∴a>6.
点评 本题考查了一元一次不等式组的整数解,根据x的取值范围,得出x的整数解,然后代入方程即可解出a的值.

练习册系列答案
相关题目
15.在一次有24 000名学生参加的数学质量抽测的成绩中,随机抽取2 000名考生的数学成绩进行分析,则在该抽样中,样本指的是( )
| A. | 所抽取的2 000名考生的数学成绩 | B. | 24 000名考生的数学成绩 | ||
| C. | 2 000 | D. | 2 000名考生 |
16.分式$\frac{1}{a+b}$,$\frac{2a}{{a}^{2}-{b}^{2}}$,$\frac{b}{b-a}$的最简公分母为( )
| A. | (a2-b2)(a+b)(b-a) | B. | (a2-b2)(a+b) | C. | (a2-b2)(b-a) | D. | a2-b2 |
13.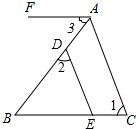 如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,∠2=55°,则∠3的度数是( )
如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,∠2=55°,则∠3的度数是( )
 如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,∠2=55°,则∠3的度数是( )
如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,∠2=55°,则∠3的度数是( )| A. | 50° | B. | 53° | C. | 55° | D. | 58° |
15.在平面直角坐标系中,函数y=-x-1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
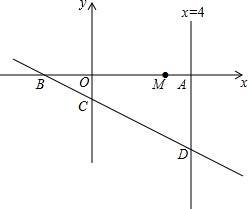 平面直角坐标系中,直线y=-$\frac{1}{2}$x-1与x轴和y轴分别交于B、C两点,与直线x=4交于点D,直线x=4与x轴交于点A,点M(3,0),点E为直线x=4上一动点,点F为直线y=-$\frac{1}{2}$x-1上一动点,ME+EF最小值为$\frac{7\sqrt{5}}{5}$,此时点F的坐标为($\frac{18}{5}$,-$\frac{14}{5}$).
平面直角坐标系中,直线y=-$\frac{1}{2}$x-1与x轴和y轴分别交于B、C两点,与直线x=4交于点D,直线x=4与x轴交于点A,点M(3,0),点E为直线x=4上一动点,点F为直线y=-$\frac{1}{2}$x-1上一动点,ME+EF最小值为$\frac{7\sqrt{5}}{5}$,此时点F的坐标为($\frac{18}{5}$,-$\frac{14}{5}$).