题目内容
7．
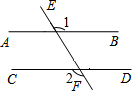如图，直线AB，CD被EF所截，且AB∥CD，若∠1=126°，则∠2=126°．
分析 先由对顶角相等可得：∠3=∠1=126°，然后由两直线平行同位角相等可得：∠2=∠3=126°．
解答 解：如图所示，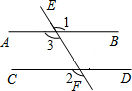
∵∠3=∠1，∠1=126°，
∴∠3=126°，
∵AB∥CD，
∴∠2=∠3=126°，
故答案为：126°．
点评 此题考查了平行线的性质，解题的关键是：熟记两直线平行同位角相等，两直线平行内错角相等，两直线平行同旁内角互补．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12．
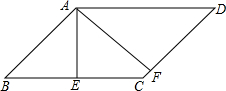如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠EAF=45°，且AE+AF=2$\sqrt{2}$，则平行四边形ABCD的周长是（ ）
如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠EAF=45°，且AE+AF=2$\sqrt{2}$，则平行四边形ABCD的周长是（ ）| A． | 2 | B． | 4$\sqrt{2}$ | C． | 4 | D． | 8 |
15．在一次有24 000名学生参加的数学质量抽测的成绩中，随机抽取2 000名考生的数学成绩进行分析，则在该抽样中，样本指的是（ ）
| A． | 所抽取的2 000名考生的数学成绩 | B． | 24 000名考生的数学成绩 | ||
| C． | 2 000 | D． | 2 000名考生 |
12．在?ABCD中，已知∠A-∠B=20°，则∠C=（ ）
| A． | 60° | B． | 80° | C． | 100° | D． | 120° |
16．分式$\frac{1}{a+b}$，$\frac{2a}{{a}^{2}-{b}^{2}}$，$\frac{b}{b-a}$的最简公分母为（ ）
| A． | （a2-b2）（a+b）（b-a） | B． | （a2-b2）（a+b） | C． | （a2-b2）（b-a） | D． | a2-b2 |
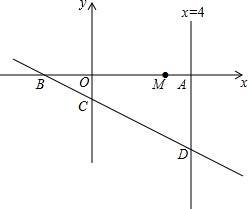平面直角坐标系中，直线y=-$\frac{1}{2}$x-1与x轴和y轴分别交于B、C两点，与直线x=4交于点D，直线x=4与x轴交于点A，点M（3，0），点E为直线x=4上一动点，点F为直线y=-$\frac{1}{2}$x-1上一动点，ME+EF最小值为$\frac{7\sqrt{5}}{5}$，此时点F的坐标为（$\frac{18}{5}$，-$\frac{14}{5}$）．