题目内容
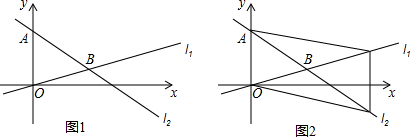
2.如图1,在直角坐标系中,点A坐标为(0,12),经过原点的直线l1与经过点A的直线l2相交于点B(m,n)(1)若m=9,n=3,求直线l1和l2的解析式;
(2)将△BAO绕点B顺时针旋转180°得△BFE,
如图2,连接AE,OF;
①证明:四边形OFEA是平行四边形;
②若四边形OFEA是正方形,则m=6,n=6.
分析 (1)由条件可得出B点坐标,结合A点坐标,利用待定系数法可求得两直线解析式;
(2)①由旋转的性质可得AB=BF、BO=BE,可证明四边形OFEA是平行四边形;②过B作BM⊥x轴于M,作BN⊥y轴于N,由正方形的性质可知BM=BN=$\frac{1}{2}$OA,可求得答案.
解答 解:
(1)由题意可知B(9,3),
设直线l1的解析式为y=kx,则3=9k,解得k=$\frac{1}{3}$,
∴直线l1的解析式为y=$\frac{1}{3}$x;
设直线l2的解析式为y=ax+b,
把A、B两点坐标代入可得$\left\{\begin{array}{l}{b=12}\\{k=-1}\end{array}\right.$,
∴直线l2的解析式为y=-x+12;
(2)①∵将△BAO绕点B顺时针旋转180°得△BFE,
∴AB=BF、BO=BE,
∴四边形OFEA是平行四边形;
②如图,过B作BM⊥x轴于M,作BN⊥y轴于N,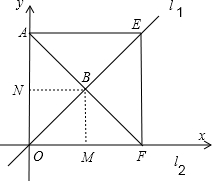
∵四边形OFEA为正方形,
∴B为AF的中点,M为OF的中点,
∴BM=$\frac{1}{2}$OA=6,
∵N为AO的中点,△ABO为直角三角形,
∴BN=$\frac{1}{2}$AO=6,
∴m=6,n=6,
故答案为:6;6.
点评 本题为一次函数的综合应用,涉及待定系数法、函数图象的交点、平行四边形的判定、正方形的性质、直角三角形的性质及三角形中位线定理等知识.在(1)中注意待定系数法的应用,在(2)①中根据旋转的性质得到四边形的对角线互相平分是解题的关键,在②中利用正方形的性质求得B点坐标是解题的关键.本题考查知识点较多,综合性较强,但难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.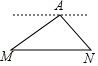 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
 如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )
如图,在海拔200米的小山顶A处,观察M,N两地,俯角分别为30°,45°,则M,N两地的距离为( )| A. | 200米 | B. | 200$\sqrt{3}$米 | C. | 400米 | D. | 200($\sqrt{3}+1$)米 |
12.数轴上的两点之间的距离为7,一个点表示的数是-3,则另一个点表示的数是( )
| A. | 4 | B. | 4或-10 | C. | -10 | D. | 10或-4 |
10.根据如表回答下列问题:
(1)275.56的平方根是±16.6;
(2)$\sqrt{2.8224}$=1.68;
(3)$\sqrt{270}$在哪两个相邻数之间?为什么?
| x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(2)$\sqrt{2.8224}$=1.68;
(3)$\sqrt{270}$在哪两个相邻数之间?为什么?
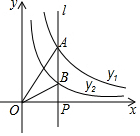 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2的值为( )
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2的值为( )