题目内容
10．
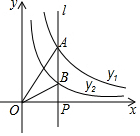如图，直线l⊥x轴于点P，且与反比例函数y1=$\frac{{k}_{1}}{x}$（x＞0）及y2=$\frac{{k}_{2}}{x}$（x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为2，则k1-k2的值为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | -4 |
分析 根据反比例函数k的几何意义可知：△AOP的面积为$\frac{{k}_{1}}{2}$，△BOP的面积为$\frac{{k}_{2}}{2}$，由题意可知△AOB的面积为$\frac{{k}_{1}}{2}-\frac{{k}_{2}}{2}$．
解答 解：根据反比例函数k的几何意义可知：△AOP的面积为$\frac{{k}_{1}}{2}$，△BOP的面积为$\frac{{k}_{2}}{2}$，
∴△AOB的面积为$\frac{{k}_{1}}{2}-\frac{{k}_{2}}{2}$，
∴$\frac{{k}_{1}}{2}-\frac{{k}_{2}}{2}$=2，
∴k1-k2=4，
故选（C）
点评 本题考查反比例函数k的几何意义，解题的关键是正确理解k的几何意义，本题属于中等题型，
练习册系列答案
相关题目
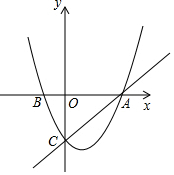如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B．C三点，点A的坐标是（3，0），抛物线的对称轴为直线x=1．
如图，二次函数y=ax2+bx+2的图象与x轴交于点A（-1，0）、B（4，0），与y轴正半轴交于点C．