题目内容
 如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.若AB=15,AD=7,BC=5,则CE的长( )
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.若AB=15,AD=7,BC=5,则CE的长( )| A、4 | ||
| B、3 | ||
C、
| ||
D、
|
考点:角平分线的性质,全等三角形的判定与性质
专题:计算题
分析:由AC平分∠BAD,CE⊥AB,CF⊥AD,根据角平分线定理得CE=CF,则利用“HL”可分别证明Rt△ACE≌Rt△ACF,Rt△CEB≌Rt△CFD,得到AE=AF,BE=DF,所以AB=AE+BE=AF+BE=AD+DF+BE=AD+2BE,则可计算出BE=4,然后在Rt△BCE中利用勾股定理可计算出CE.
解答:解:∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,
在Rt△ACE和Rt△ACF中,
,
∴Rt△ACE≌Rt△ACF(HL),
∴AE=AF,
在Rt△CEB和Rt△CFD中,
,
∴Rt△CEB≌Rt△CFD(HL),
∴BE=DF,
∴AB=AE+BE=AF+BE=AD+DF+BE=AD+2BE,
∴BE=
(AB-AD)=
×(15-7)=4,
在Rt△BCE中,∵BC=5,BE=4,
∴CE=
=3.
故选B.
∴CE=CF,
在Rt△ACE和Rt△ACF中,
|
∴Rt△ACE≌Rt△ACF(HL),
∴AE=AF,
在Rt△CEB和Rt△CFD中,
|
∴Rt△CEB≌Rt△CFD(HL),
∴BE=DF,
∴AB=AE+BE=AF+BE=AD+DF+BE=AD+2BE,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BCE中,∵BC=5,BE=4,
∴CE=
| BC2-BE2 |
故选B.
点评:本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
如图,如果从半径为5cm的圆形纸片上剪去
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
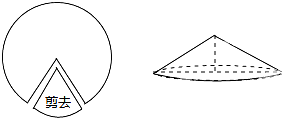
| 1 |
| 5 |

| A、1cm | ||
| B、3cm | ||
C、2
| ||
| D、4cm |
在等腰三角形中,有一个角是30°,它的一条腰上的高与底边的夹角是( )
| A、15° |
| B、15°或60° |
| C、30°或60° |
| D、60° |
在Rt△ABC中,如果各边的长度都缩小至原来的
,那么锐角A的各个三角函数值( )
| 1 |
| 4 |
A、都缩小
| ||
| B、都扩大4倍 | ||
| C、都不变 | ||
| D、无法确定 |
多项式x2-3x+a可分解为(x-5)(x-b),则a、b的值分别是( )
| A、10和-2 |
| B、-10和2 |
| C、10和2 |
| D、-10和-2 |
 小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料,小聪骑电动车,小明骑自行车,当小聪从原路回到学校时,小明刚好到市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(小时)之间的函数关系,请根据图象回答下列问题:
小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料,小聪骑电动车,小明骑自行车,当小聪从原路回到学校时,小明刚好到市图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(小时)之间的函数关系,请根据图象回答下列问题: