题目内容
多项式x2-3x+a可分解为（x-5）（x-b），则a、b的值分别是（ ）
| A、10和-2 |
| B、-10和2 |
| C、10和2 |
| D、-10和-2 |
考点：因式分解-十字相乘法等
专题：
分析：利用多项式乘法整理多项式进而得出a，b的值．
解答：解：∵多项式x2-3x+a可分解为（x-5）（x-b），
∴x2-3x+a=（x-5）（x-b）=x2-（b+5）x+5b，
故b+5=3，5b=a，
解得：b=-2，a=-10．
故选：B．
∴x2-3x+a=（x-5）（x-b）=x2-（b+5）x+5b，
故b+5=3，5b=a，
解得：b=-2，a=-10．
故选：B．
点评：此题主要考查了整式的混合运算，得出同类项系数相等是解题关键．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
张老师想了解山东省第20届七年级数学竞赛的成绩中几个不同学校获一等奖的同学数的百分数，你觉得用哪一个统计图比较合适（ ）
| A、折线统计图 |
| B、扇形统计图 |
| C、条形统计图 |
| D、以上都可以 |
如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD．若AB=15，AD=7，BC=5，则CE的长（ ）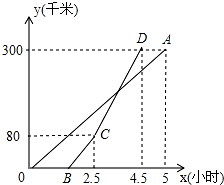
甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发开往乙地．如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与x（小时）之间的函数关系．请根据图象解答下列问题：
如图是某年1月份的日历，小红用平行四边形从中任意的框出三个日期，若这三个日期这和是48，则C处的日期为1月（ ）日．
| A、24 | B、25 | C、26 | D、23 |
两个同样大小的正方体积木，每个正方体相对两个面上写的数字之和都等于0．现将两个正方体并排放置，看得见的5个面上的数如图所示，则看不见的7个面上所写的数字之和等于能说明命题“如果两个角互补，那么这两个角一个是锐角，另一个是钝角”为假命题的两个角是（ ）
| A、120°，60° |
| B、95°，105° |
| C、30°，60° |
| D、90°，90° |
如下图：点A在双曲线y=