题目内容
2. 如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且DF=2$\sqrt{3}$,以O为圆心,OC为半径作弧CE,交OB于点E.
如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且DF=2$\sqrt{3}$,以O为圆心,OC为半径作弧CE,交OB于点E.(1)求OA的长;
(2)计算阴影部分的面积.
分析 (1)首先证明OA⊥DF,由垂径定理求出CD=$\sqrt{3}$,由OD=2CO推出∠CDO=30°,设OC=x,则OD=2x,利用勾股定理即可解决问题.
(2)根据S阴=S△CDO+S扇形OBD-S扇形OCE计算即可.
解答 解;(1)连接OD,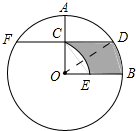 ∵OA⊥OB,
∵OA⊥OB,
∴∠AOB=90°,
∵CD∥OB,
∴∠OCD=90°,∴OA⊥DF,∴CD=$\frac{1}{2}$DF=$\sqrt{3}$
在Rt△OCD中,∵C是AO中点,
∴OA=OD=2CO,
设OC=x,
则x2+( $\sqrt{3}$)2=(2x)2,
解得:x=1,
∴OA=OD=2,
(2)∵OC=$\frac{1}{2}$OD,∠OCD=90°,∴∠CDO=30°,
∵FD∥OB,
∴∠DOB=∠ODC=30°,
∴S阴=S△CDO+S扇形OBD-S扇形OCE
=$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{30π×{2}^{2}}{360}$-$\frac{90π×{1}^{2}}{360}$=$\frac{{\sqrt{3}}}{2}+\frac{π}{12}$.
点评 本题考查了扇形面积、垂径定理、勾股定理、有一个角是30度的直角三角形的性质等知识,解题的关键是学会利用分割法求面积.学会把求不规则图形面积转化为求规则图形面积,属于中考常考题型.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
12.不能判定四边形ABCD是平行四边形的条件是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,∠B=∠D | C. | ∠A=∠B,∠C=∠D | D. | AB=CD,∠BAC=∠ACD |
14.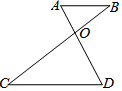 如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
 如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )
如图,己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$,△AOB的面积是100 cm2,则△DOC的面积为( )| A. | 200 cm2 | B. | 300 cm2 | C. | 400 cm2 | D. | 500 cm2 |
 如图,在△ABC中,AB=AC,外角∠ACD=110°,则∠B的度数为70°.
如图,在△ABC中,AB=AC,外角∠ACD=110°,则∠B的度数为70°. 如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.
如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.