题目内容
11.计算下列各式的值:$\sqrt{{9}^{2}+19}$;$\sqrt{9{9}^{2}+199}$;$\sqrt{99{9}^{2}+1999}$;$\sqrt{999{9}^{2}+19999}$观察所得结果,总结存在的规律,应用得到的规律计算$\sqrt{\underset{\underbrace{99…{9}^{2}}}{2016个9}+\underset{\underbrace{199…9}}{2016个9}}$.分析 直接计算各式进而得出规律求出答案.
解答 解:$\sqrt{{9}^{2}+19}$=10;$\sqrt{9{9}^{2}+199}$=100;
$\sqrt{99{9}^{2}+1999}$=1000;$\sqrt{999{9}^{2}+19999}$=10000,
观察所得结果,可得$\sqrt{\underset{\underbrace{99…{9}^{2}}}{2016个9}+\underset{\underbrace{199…9}}{2016个9}}$=102016.
点评 此题主要考查了二次根式的性质与化简,正确得出规律是解题关键.

练习册系列答案
相关题目
 如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且DF=2$\sqrt{3}$,以O为圆心,OC为半径作弧CE,交OB于点E.
如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且DF=2$\sqrt{3}$,以O为圆心,OC为半径作弧CE,交OB于点E. 如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.
如图,一块矩形绿地ABCD由篱笆围着,并且由一条与AB边平行的篱笆EF分开,已知AB=xm,篱笆的总长为600m.

 如图AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于点E,F为AD的中点,连结EF.
如图AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于点E,F为AD的中点,连结EF.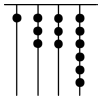 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )