题目内容
12．不能判定四边形ABCD是平行四边形的条件是（ ）| A． | AB=CD，AD=BC | B． | AB∥CD，∠B=∠D | C． | ∠A=∠B，∠C=∠D | D． | AB=CD，∠BAC=∠ACD |
分析 根据平行四边形的判断定理分别作出判断得出即可．
解答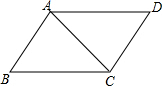 
解：A、“AB=CD，AD=BC”是四边形ABCD的两组对边分别相等，可以判定四边形ABCD是平行四边形，故本选项错误；
B、“AB∥CD，∠B=∠D”是四边形ABCD的一组对边平行，一组对角相等，不可以判定四边形ABCD是平行四边形，故本选项正确；
C、“∠A=∠C，∠B=∠D”是四边形ABCD的两组对角相等，可以判定四边形ABCD是平行四边形，故本选项错误；
B、“AB∥CD，AD=BC”是四边形ABCD的一组对边平行，另一组对边相等，不可以判定四边形ABCD是平行四边形，故本选项错误；
D、由∠BAC=∠ACD可以推知AB∥CD，结合AB=CD，根据四边形ABCD的一组对边平行且相等，可以判定四边形ABCD是平行四边形，故本选项错误．
故选：B．
点评 此题主要考查了平行四边形的判定定理，准确无误的掌握定理是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．
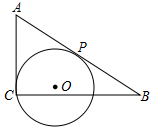如图，在Rt△ACB中，∠ACB=90°，AC=3，BC=4，有一过点C的动圆⊙O与斜边AB相切于动点P，则⊙O的半径r的最大值与最小值之差为（ ）
如图，在Rt△ACB中，∠ACB=90°，AC=3，BC=4，有一过点C的动圆⊙O与斜边AB相切于动点P，则⊙O的半径r的最大值与最小值之差为（ ）| A． | $\frac{10}{3}$ | B． | $\frac{8}{5}$ | C． | $\frac{32}{15}$ | D． | $\frac{25}{12}$ |
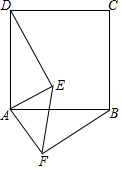如图，正方形ABCD内一点E，△ADE绕点A顺时针旋转能与△ABF重合，若AE=3，求∠EAF的度数和EF的长．
如图，在⊙O中，半径OA⊥OB，过OA的中点C作FD∥OB交⊙O于D、F两点，且DF=2$\sqrt{3}$，以O为圆心，OC为半径作弧CE，交OB于点E．