题目内容
14．
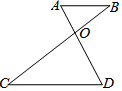如图，己知$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$，△AOB的面积是100 cm2，则△DOC的面积为（ ）| A． | 200 cm2 | B． | 300 cm2 | C． | 400 cm2 | D． | 500 cm2 |
分析 根据$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$，∠AOB=∠COD，证明△AOB∽△COD，利用相似三角形的面积比等于相似比的平方即可求出答案．
解答 解：∵$\frac{OA}{DO}$=$\frac{BO}{CO}$=$\frac{1}{2}$，
∠AOB=∠COD，
∴△AOB∽△COD，
∴$\frac{{S}_{△AOB}}{{S}_{△COD}}=（\frac{OA}{DO}）^{2}$，
∴S△DOC=400
故选（C）
点评 本题考查相似三角形的判定与性质，解题的关键是证明△AOB∽△COD，本题属于基础题型．
练习册系列答案
相关题目
5．下列各式的值一定是正数的是（ ）
| A． | |a| | B． | $\sqrt{a^2}$ | C． | $\frac{1}{a^2}$ | D． | $\root{3}{a}$ |
如图，在⊙O中，半径OA⊥OB，过OA的中点C作FD∥OB交⊙O于D、F两点，且DF=2$\sqrt{3}$，以O为圆心，OC为半径作弧CE，交OB于点E．
9．
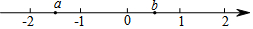实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）
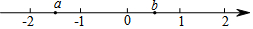实数a，b在数轴上的位置如图所示，以下说法正确的是（ ）| A． | a+b＞0 | B． | a-b＞0 | C． | $\frac{a}{b}$＞0 | D． | b2＜a2 |
如图，一块矩形绿地ABCD由篱笆围着，并且由一条与AB边平行的篱笆EF分开，已知AB=xm，篱笆的总长为600m．
4．若一次函数y=kx+2经过点（-1，1），则下面说法正确的是（ ）
| A． | y随x的增大而增大 | B． | 图象经过点（3，-1） | ||
| C． | 图象不经过第二象限 | D． | 图象与函数y=-x图象有一个交点 |