题目内容
17.某校组织夏令营活动,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则刚好坐满;若只租用42座客车,则能少租一辆,而且还有一辆没有坐满,但超过30人,问:(1)该校有多少人参加夏令营活动?
(2)已知36座客车每辆租金400元,42座客车每辆租金440元,请你帮该校设计一种最省钱得租车方案.
分析 (1)设租36座的车x辆,则租42座的客车(x-1)辆.不等关系:租42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人.
(2)根据(1)中求得的人数,进一步计算三种方案的费用:①只租36座客车;②只租42座客车;③合租两种车.再进一步比较得到结论即可.
解答 解:设租用36座客车x辆,则总人数是36x人,
由题意列式为:
30<36x-42(x-2)<42,
解得:7<x<9,
x取整数为:x=8,
参加人数为36×8=288人,
答:该校有288人参加夏令营活动;
(2)方案一:8×400=3200,
方案二:(8-1)×440=3080,
方案三:∵42×6+36=288,
∴6×440+400=3040,
3040<3080<3200,
因此选择方案三更合算.
点评 此题主要考查了一元一次不等式组的应用,理解此题中的不等关系是解决此题的重点,特别注意要能够分别求得每一种方案的价钱,再作比较.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,在下列说法中,错误的是( )
| A. | 如果增加条件AC=A′C′,那么△ABC≌△A′B′C′(SAS) | |
| B. | 如果增加条件BC=B′C′,那么△ABC≌△A′B′C′(SAS) | |
| C. | 如果增加条件∠B=∠B′,那么△ABC≌△A′B′C′(ASA) | |
| D. | 如果增加条件∠C=∠C′,那么△ABC≌△A′B′C′(AAS) |
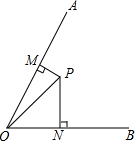 如图,∠AOB=60°,P为∠AOB内一点,P到OA、OB的距离PM、PN分别为2和11,求OP的长.
如图,∠AOB=60°,P为∠AOB内一点,P到OA、OB的距离PM、PN分别为2和11,求OP的长.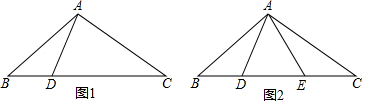
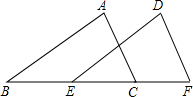 如图,已知△ABC≌△DEF,AB与DE是对应边,∠ACB与∠F是对应角.
如图,已知△ABC≌△DEF,AB与DE是对应边,∠ACB与∠F是对应角.