题目内容
12.设[t]表示不超过实数t的最大整数,令{t}=t-[t].已知实数x满足x3+$\frac{1}{{x}^{3}}$=18,则{x}+{$\frac{1}{x}$}=( )| A. | $\frac{1}{2}$ | B. | 3$-\sqrt{5}$ | C. | $\frac{1}{2}$(3$-\sqrt{5}$) | D. | 1 |
分析 根据题意得出[x]=2,进而利用x3+$\frac{1}{{x}^{3}}$=(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)求出x+$\frac{1}{x}$的值,进而求出答案.
解答 解:设x>$\frac{1}{x}$,
∵x3+$\frac{1}{{x}^{3}}$=18>0,
∴x>$\frac{1}{x}$>0,
易知[$\frac{1}{x}$]=0,而对于x3+$\frac{1}{{x}^{3}}$=18来说,
0<$\frac{1}{{x}^{3}}$<1,
∴17<x3<18,
∴[x]=2,
而x3+$\frac{1}{{x}^{3}}$
=(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)
=(x+$\frac{1}{x}$)[(x+$\frac{1}{x}$)2-3]
令t=x+$\frac{1}{x}$,
则t3-3t-18=0,
(t-3)(t2+3t+6)=0,
解得:t=3,
∴{x}+{$\frac{1}{x}$}=x+$\frac{1}{x}$-[x]-[$\frac{1}{x}$]=t-2-0=3-2=1.
故选:D.
点评 此题主要考查了取整计算,正确根据题意得出{x}+{$\frac{1}{x}$}=x+$\frac{1}{x}$-[x]-[$\frac{1}{x}$]是解题关键.

练习册系列答案
相关题目

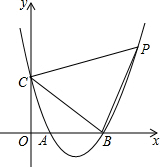 如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标.
如图,抛物线y=x2-4x+3与坐标轴交于A,B,C三点,点P为对称轴右侧的抛物线上一点,若tan∠PCB=2,求P点坐标. 已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.
已知,如图,AD是△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,求证:AB=AC.