题目内容
18.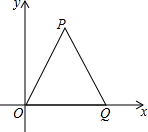 如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.
如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.(1)求等边三角形边长;
(2)求点P坐标及反比例函数解析式.
分析 (1)设等边三角形的边长为x,过点P作PD⊥OQ于点D,根据锐角三角函数的定义用x表示出PD的长,再由三角形的面积公式即可得出x的值;
(2)根据PD的长及等边三角形的性质求出OD的长,故可得出P点坐标,利用待定系数法即可得出反比例函数的解析式.
解答 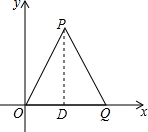 解:(1)设等边三角形的边长为x,过点P作PD⊥OQ于点D,
解:(1)设等边三角形的边长为x,过点P作PD⊥OQ于点D,
∵OP=x,∠POD=60°,
∴PD=OP•sin60°=$\frac{\sqrt{3}}{2}$x.
∵△OPQ是面积为4$\sqrt{3}$,
∴$\frac{1}{2}$x•$\frac{\sqrt{3}}{2}$x=4$\sqrt{3}$,解得x=4.
答:等边△OPQ的边长是4;
(2)∵由(1)知OQ=4,
∴OD=2,PD=$\frac{\sqrt{3}}{2}$×4=2$\sqrt{3}$,
∴P(2,2$\sqrt{3}$).
设反比例函数的解析式为y=$\frac{k}{x}$,
∴k=xy=2×2$\sqrt{3}$=4$\sqrt{3}$,
∴反比例函数解析式为y=$\frac{4\sqrt{3}}{x}$.
点评 本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
相关题目
3.若反比例函数的图象过点(-2,2),则k的值是( )
| A. | 2 | B. | -4 | C. | 0 | D. | 4 |
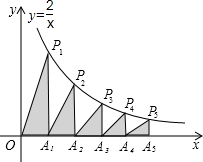 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5=1,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为$\frac{137}{60}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5=1,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为$\frac{137}{60}$.