题目内容
9.下面是按一定规律徘列的一列数:第1个式子:1-(1+$\frac{-1}{2}$)
第2个式子:2-(1+$\frac{-1}{2}$)[1+$\frac{(-1)^{2}}{3}$][1+$\frac{(-1)^{3}}{4}$];
第3个式子:3-(1+$\frac{-1}{2}$))[1+$\frac{(-1)^{2}}{3}$][1+$\frac{(-1)^{3}}{4}$][1+$\frac{(-1)^{4}}{5}$][1+$\frac{(-1)^{5}}{6}$];…
(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2015个式子的形式(中间部分用省略号,两端部分必须写详细),然后推测出结果.
分析 (1)直接计算这三个数的结果即可;
(2)由以上算式可以看出第n个式子为:n-(1+$\frac{-1}{2}$)(1+$\frac{(-1)^{2}}{3}$)(1+$\frac{(-1)^{3}}{4}$)…(1+$\frac{(-1)^{2n-1}}{2n}$),再将n=2015代入即可.
解答 解:(1)第1个式子:1-(1+$\frac{-1}{2}$)=$\frac{1}{2}$;
第2个式子:2-(1+$\frac{-1}{2}$)[1+$\frac{(-1)^{2}}{3}$][1+$\frac{(-1)^{3}}{4}$]=$\frac{3}{2}$;
第3个式子:3-(1+$\frac{-1}{2}$)[1+$\frac{(-1)^{2}}{3}$][1+$\frac{(-1)^{3}}{4}$][1+$\frac{(-1)^{4}}{5}$][1+$\frac{(-1)^{5}}{6}$]=$\frac{5}{2}$;
(2)第2015个式子:2015-(1+$\frac{-1}{2}$)(1+$\frac{(-1)^{2}}{3}$)(1+$\frac{(-1)^{3}}{4}$)…(1+$\frac{(-1)^{4028}}{4029}$)(1+$\frac{(-1)^{4029}}{4030}$)
=2015-$\frac{1}{2}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{6}{5}$×$\frac{5}{6}$×…×$\frac{4030}{4029}$×$\frac{4029}{4030}$
=2015-$\frac{1}{2}$
=$\frac{4029}{2}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

| A. | 8 | B. | -8 | C. | ±8 | D. | 以上答案都不对 |
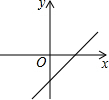 一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
一次函数y=kx-b的图象如图所示,则下列结论正确的是( )| A. | k>0,b<0 | B. | k>0,b>0 | C. | k<0,b<0 | D. | k<0,b>0 |
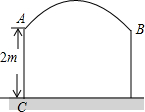 某村想在村口建一个如图形状的牌门,已知弧$\widehat{AB}$是所在圆的三分之一圆,立柱AC高2m,若要使高3m,宽2m的集装箱货车能通过,问AB的半径应大于多少m?
某村想在村口建一个如图形状的牌门,已知弧$\widehat{AB}$是所在圆的三分之一圆,立柱AC高2m,若要使高3m,宽2m的集装箱货车能通过,问AB的半径应大于多少m?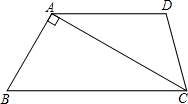 如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AC的长.
如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AC的长.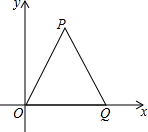 如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.
如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.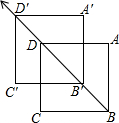 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )