题目内容
8.二次函数y=-$\frac{1}{3}$(x-1)(x+3)的图象的对称轴是直线x=-1.分析 由函数 y=-$\frac{1}{3}$(x-1)(x+3)可得出此函数与x轴的交点,再根据这两点关于对称轴对称即可求出其对称轴方程
解答 解:∵y=-$\frac{1}{3}$(x-1)(x+3)与x轴的两交点为(1,0),(-3,0),
∴其对称轴x=$\frac{-3+1}{2}$=-1.
故答案为:x=-1.
点评 本题考查的是二次函数的性质,熟知二次函数的对称轴方程及函数图象与x轴的交点问题是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
19.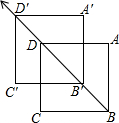 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )| A. | 25 | B. | 39 | C. | 47 | D. | 49 |
17.下列合并同类项,结果正确的是( )
| A. | x4+x4=x8 | B. | 5m-2m+4m=7m | ||
| C. | 15a+4a-11=18a | D. | -9xy-2xy+11xy=xy |
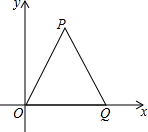 如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.
如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P. 用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?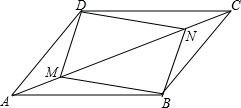 已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN.求证:四边形BMDN是平行四边形.
已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN.求证:四边形BMDN是平行四边形.