题目内容
7.某同学在计算多边形的内角和时少加了一个内角的度数,得到的答案是1125°,求这个多边形的边数是多少?少加的那个内角的度数是多少?分析 先设出少加的内角的度数,然后依据多边形的内角和公式列出方程,然后根据0°<x<180°列出不等式,从而可求得n的值,然后可求得x的值.
解答 解:设少加的度数为x°此多边形为n边形.
∵1125°+x=(n-2)×180°,
∴x=180°×(n-2)-1125°,
∵0°<x<180°,
∴0<180°×(n-2)-1125°<180,
∴8.2<n<9.3,
∴n=9,
∴x=180°×(9-2)-1125°=135°.
∴此多边形是九边形,少加的那个内角的度数是135°.
点评 本题考查的是多边形的内角和公式.解答此题的关键是把所求的角正确的分解为180°与一个正整数的积再减去一个小于180°的角的形式,再根据多边形的内角和公式即可求解.

练习册系列答案
相关题目
17.已知x轴上一点A(6,0),y轴上一点B(0,b),且AB=10,则b的值为( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 以上答案都不对 |
19.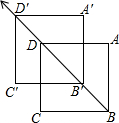 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )| A. | 25 | B. | 39 | C. | 47 | D. | 49 |
17.下列合并同类项,结果正确的是( )
| A. | x4+x4=x8 | B. | 5m-2m+4m=7m | ||
| C. | 15a+4a-11=18a | D. | -9xy-2xy+11xy=xy |
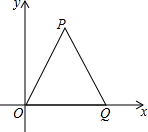 如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.
如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.