题目内容
13.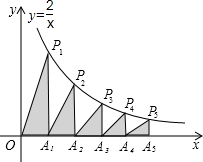 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5=1,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为$\frac{137}{60}$.
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5=1,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S1+S2+S3+S4+S5的值为$\frac{137}{60}$.
分析 由于过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|,可先由|k|依次表示出图中各阴影三角形的面积,再相加即可得到面积的和.
解答 解:由于OA1=A1A2=A2A3=A3A4=A4A5,S1=$\frac{1}{2}$|k|,S2=$\frac{1}{4}$|k|,S3=$\frac{1}{6}$|k|,S4=$\frac{1}{8}$|k|,S5=$\frac{1}{10}$|k|;
则S1+S2+S3+S4+S5=($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$+$\frac{1}{10}$)|k|=$\frac{60+30+20+15+12}{120}$×2=$\frac{137}{60}$.
故答案为:$\frac{137}{60}$.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.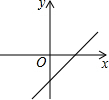 一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
 一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
一次函数y=kx-b的图象如图所示,则下列结论正确的是( )| A. | k>0,b<0 | B. | k>0,b>0 | C. | k<0,b<0 | D. | k<0,b>0 |
8.2的算术平方根是( )
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | ±2 |
5.下列条件中,不能判定△ABC为直角三角形的是( )
| A. | ∠A+∠B=90° | B. | a2+b2=c2 | C. | a:b:c=3:4:5 | D. | ∠A:∠B:∠c=3:4:5 |
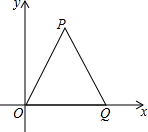 如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.
如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.