题目内容
6.(1)$\sqrt{12}+\sqrt{20}-(\sqrt{5}-\sqrt{3})$(2)$\sqrt{\frac{2}{3}}÷\sqrt{2\frac{2}{3}}×\sqrt{\frac{2}{5}}$
(3)$\sqrt{24}+3\sqrt{\frac{2}{3}}-\sqrt{9}$
(4)$\sqrt{2}×\sqrt{8}+\frac{{\sqrt{32}}}{{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}}$.
分析 (1)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(2)根据二次根式的乘除法则运算;
(3)先把各二次根式化简,然后合并即可;
(4)先进行二次根式的乘法运算,然后化简即可.
解答 解:(1)原式=2$\sqrt{3}$+2$\sqrt{5}$-$\sqrt{5}$+$\sqrt{3}$
=3$\sqrt{3}$+$\sqrt{5}$;
(2)原式=$\sqrt{\frac{2}{3}×\frac{3}{8}×\frac{2}{5}}$
=$\frac{\sqrt{10}}{10}$;
(3)原式=2$\sqrt{6}$+$\sqrt{6}$-3
=3$\sqrt{6}$-3;
(4)原式=$\sqrt{2×8}$+$\frac{4\sqrt{2}}{5-3}$
=4+2$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
16.下列方程有解的是( )
| A. | x-1=1-x | B. | x+4=x-4 | C. | |x+1|+1=0 | D. | 2(x+2)=2x |
17.已知x轴上一点A(6,0),y轴上一点B(0,b),且AB=10,则b的值为( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 以上答案都不对 |
1.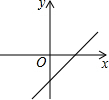 一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
 一次函数y=kx-b的图象如图所示,则下列结论正确的是( )
一次函数y=kx-b的图象如图所示,则下列结论正确的是( )| A. | k>0,b<0 | B. | k>0,b>0 | C. | k<0,b<0 | D. | k<0,b>0 |
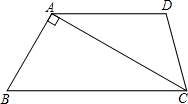 如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AC的长.
如图,在梯形ABCD中,AD∥BC,∠B=60°,∠ADC=105°,AD=6,且AC⊥AB,求AC的长.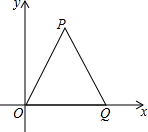 如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.
如图,△OPQ是面积为4$\sqrt{3}$的等边三角形,若反比例函数的图象过点P.