题目内容
 如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.
如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.(1)求证:四边形CEDF是平行四边形;
(2)①当AE=
②当AE=
考点:平行四边形的判定与性质,全等三角形的判定与性质,菱形的判定,矩形的判定
专题:
分析:(1)证△CFG≌△EDG,推出FG=EG,根据平行四边形的判定推出即可;
(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;
②求出△CDE是等边三角形,推出CE=DE,根据菱形的判定推出即可.
(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;
②求出△CDE是等边三角形,推出CE=DE,根据菱形的判定推出即可.
解答:(1)证明:四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
又∠CGF=∠EGD.
G是CD的中点,
CG=DG,
在△FCG和△EDG中,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5;
②当AE=2时,四边形CEDF是菱形,
理由是:∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:2.
∴CF∥ED,
∴∠FCD=∠GCD,
又∠CGF=∠EGD.
G是CD的中点,
CG=DG,
在△FCG和△EDG中,
|
∴△CFG≌△EDG(ASA),
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;

(2)①解:当AE=3.5时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,
|
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5;
②当AE=2时,四边形CEDF是菱形,
理由是:∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:2.
点评:本题考查了平行四边形的性质和判定,菱形的判定,矩形的判定,等边三角形的性质和判定,全等三角形的性质和判定的应用,注意:有一组邻边相等的平行四边形是菱形,有一个角是直角的平行四边形是矩形.

练习册系列答案
相关题目

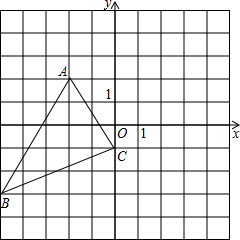 如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题: 一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件. 如图,已知BC为⊙O的直径,A为⊙O上一点,连接AB、AC,BC=4,tanB=2,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于E点.
如图,已知BC为⊙O的直径,A为⊙O上一点,连接AB、AC,BC=4,tanB=2,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于E点. 如图,△ABC在平面直角坐标系中:
如图,△ABC在平面直角坐标系中: