题目内容
有多少个小于2008的数，使得它们与72相乘均为完全平方数．
考点：完全平方数
专题：
分析：首先得出72×2×12，72×2×22，72×2×32…，进而得出完全平方数＜1004，进而得出答案．
解答：解：72=62×2要让结果是完全平方数，所以乘以2是完全平方数，
则72×2×12，72×2×22，72×2×32…，
∵2008÷2=1004，
∴完全平方数＜1004，
又∵312＜1004＜322
故有31个数．
则72×2×12，72×2×22，72×2×32…，
∵2008÷2=1004，
∴完全平方数＜1004，
又∵312＜1004＜322
故有31个数．
点评：此题主要考查了完全平方数，得出72=62×2要让结果是完全平方数，所以乘以2是完全平方数，进而求出是解题关键．
练习册系列答案
相关题目
如图，已知在等边△ABC，点D是△ABC角平分线AD、CD的交点，P为△ABC外一点上，∠APC=60°，连接DP．求证：PD平分∠APC．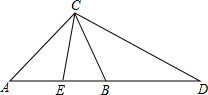
如图，CE、CB分别是△ABC与△ADC的中线，且∠ACB=∠ABC．求证：CD=2CE．