题目内容
19.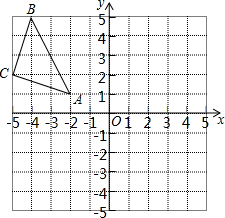 由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).(1)请作出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2;
(3)请你判断△AA1A2与△CC1C2的相似比;若不相似,请直接写出△AA1A2的面积.
分析 (1)利用关于y轴对称点的性质得出对应点位置求出即可;
(2)利用关于原点对称点的性质得出对应点坐标进而求出即可;
(3)利用相似三角形的判定方法得出即可,再利用三角形面积求法得出答案.
解答 解: (1)如图所示:△A1B1C1,即为所求;
(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵$\frac{C{C}_{1}}{A{A}_{1}}$≠$\frac{{C}_{1}{C}_{2}}{{A}_{1}{A}_{2}}$,
∴△AA1A2与△CC1C2不相似,
S△AA1A2=$\frac{1}{2}$×2×4=4.
点评 此题主要考查了关于y轴对称点的性质以及关于原点对称点的性质和相似三角形的判定等知识,得出对应点位置是解题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
14.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
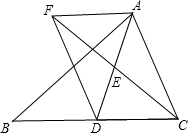 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.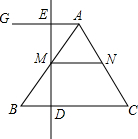 如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.
如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.