题目内容
8.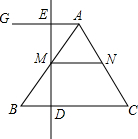 如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.
如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.(1)求证:ME=MD;
(2)N是AC的中点,且MN=5.
填空:①若AB=AC,当BD=5时,四边形AEBD是矩形;
②若AB⊥AC,当BD=5时,四边形AEBD是菱形.
分析 (1)根据平行线性质得出∠AEM=∠BDM,求出AM=BM,根据AAS推出△AEM≌△BDM即可;
(2)①根据三角形中位线求出BC长,求出四边形是平行四边形,求出∠ADB=90°,根据矩形的判定推出即可;
②根据直角三角形斜边上中线性质求出AD=DB,根据菱形的判定推出即可.
解答 (1)证明:∵AG∥BC,
∴∠AEM=∠BDM,
∵点M是AB边的中点,
∴AM=BM,
在△AEM和△BDM中,
$\left\{\begin{array}{l}{∠EMA=∠BMD}\\{∠AEM=∠BDM}\\{AM=BM}\end{array}\right.$,
∴△AEM≌△BDM,
∴ME=MD;
(2)解:①当BD=5时,四边形AEBD是矩形,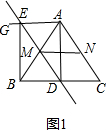
理由是:∵点M是AB边的中点,N是AC的中点,MN=5,
∴BC=2MN=10,
∴CD=BD=5,
∵AB=AC,
∴AD⊥BC,
∴∠ADB=90°,
∵EM=DM,AM=BM,
∴四边形AEBD是平行四边形,
∴四边形AEBD是矩形,
故答案为:5;
②当BD=5时,四边形AEBD是菱形,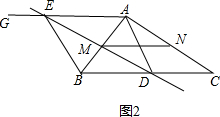
理由是:∵点M是AB边的中点,N是AC的中点,MN=5,
∴BC=2MN=10,
∴CD=BD=5,
∵AC⊥AB,
∴∠BAC=90°,
∴AD=$\frac{1}{2}$BC=5,
∴AD=BD,
∵四边形AEBD是平行四边形,
∴四边形AEBD是菱形,
故答案为:5.
点评 本题考查了平行线的性质,全等三角形的判定和性质,矩形的判定,三角形的中位线,菱形的判定,平行四边形的判定,直角三角形斜边上的中线性质,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
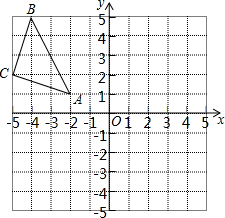 由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).
由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).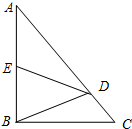 如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).
如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).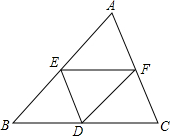 如图,E和F分别是边AB和AC中点,D是BC边上一点,若∠AED=∠AFD,请问四边形AEDF是平行四边形吗?为什么?
如图,E和F分别是边AB和AC中点,D是BC边上一点,若∠AED=∠AFD,请问四边形AEDF是平行四边形吗?为什么?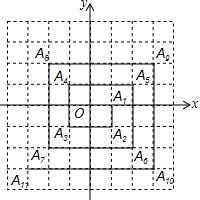 如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2014的坐标是(504,-504).
如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2014的坐标是(504,-504).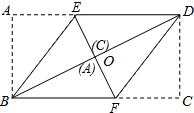 如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.
如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.