题目内容
已知关于x的分式方程
+
=
有解,求p的取值范围.
| 2 |
| x |
| 4 |
| x-1 |
| 7x+p |
| x(x-1) |
考点:分式方程的解
专题:
分析:分式方程去分母转化为整式方程,根据分式方程有解得到-p-2≠0且-p-2≠1,求出p的取值范围即可.
解答:解:方程两边同时乘以x(x-1)得:
2(x-1)+4x=7x+p,
x=-p-2,
∵关于x的分式方程
+
=
有解,
∴x≠0且x≠1,
∴-p-2≠0且-p-2≠1,
∴p≠-2且p≠-3.
2(x-1)+4x=7x+p,
x=-p-2,
∵关于x的分式方程
| 2 |
| x |
| 4 |
| x-1 |
| 7x+p |
| x(x-1) |
∴x≠0且x≠1,
∴-p-2≠0且-p-2≠1,
∴p≠-2且p≠-3.
点评:本题考查了分式方程,用到的知识点是分式方程有解的条件,关键是根据分式方程有解的条件得出-p-2≠0且-p-2≠1.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
抛物线y=-x2+2x+2绕它与y轴的交点旋转180°后得到的抛物线解析式为( )
| A、y=x2+2x+2 |
| B、y=-x2-2x+2 |
| C、y=x2+2x+1 |
| D、y=2x2+4x+2 |
 如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作
如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作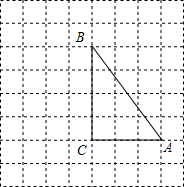 如图所示的网格中,每个小网格都是边长为1的正方形,每个小正方形的顶点叫格点,△ABC的顶点都在格点上.在AC的延长线上取一点D,D也在格点上,并连接BD.
如图所示的网格中,每个小网格都是边长为1的正方形,每个小正方形的顶点叫格点,△ABC的顶点都在格点上.在AC的延长线上取一点D,D也在格点上,并连接BD.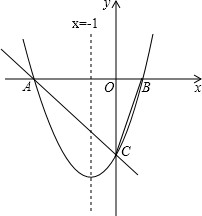 对称轴为直线x=-1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(-3,0).
对称轴为直线x=-1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(-3,0).