题目内容
等腰三角形一腰上的高与底边夹角是12°,则顶角的度数为 .
考点:等腰三角形的性质
专题:
分析:先求出底角∠B=∠ACB=78°,即可求出顶角∠A=24°.
解答:解:如图所示:
∵CD⊥AB,
∴∠BDC=90°,
∴∠B=90°-∠BCD=90°-12°=78°,
∵AB=AC,∴∠ACB=∠B=78°,
∴∠A=180°-78°-78°=24°;
即顶角度数为24°;
故答案为:24°.

∵CD⊥AB,
∴∠BDC=90°,
∴∠B=90°-∠BCD=90°-12°=78°,
∵AB=AC,∴∠ACB=∠B=78°,
∴∠A=180°-78°-78°=24°;
即顶角度数为24°;
故答案为:24°.
点评:本题考查了等腰三角形的性质和三角形内角和定理;弄清各个角之间的关系是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
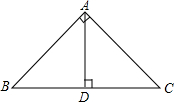 如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论:
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论:①AB与AC互相垂直
②AD与AC互相垂直
③点C到AB的垂线段是线段AB
④点A到BC的距离是线段AD
⑤线段AB的长度是点B到AC的距离
⑥线段AB是点B到AC的距离.
其中正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
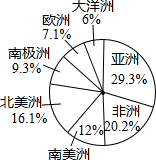 如图反映的是地球上七大洲的面积占陆地总面积的百分比,小明根据如图得出了
如图反映的是地球上七大洲的面积占陆地总面积的百分比,小明根据如图得出了下列四个结论:
①七大洲中面积最大的是亚洲;
②南美洲、北美洲、非洲三大州的面积和约占陆地总面积的50%;
③非洲约占陆地总面积的20%;
④南美洲的面积是大洋洲面积的2倍.
你认为上述四个结论中正确的应该是( )
| A、①② | B、①④ |
| C、①②④ | D、①②③④ |
 如图,用放大镜将图形放大,这种图形的改变是( )
如图,用放大镜将图形放大,这种图形的改变是( )| A、相似 | B、平移 | C、轴对称 | D、旋转 |
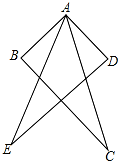 如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.
如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE. 如图,分别画出点A、B、C到BC、AC、AB的垂线段,并量出点A到BC,点B到AC,点C到AB的距离.
如图,分别画出点A、B、C到BC、AC、AB的垂线段,并量出点A到BC,点B到AC,点C到AB的距离. 如图,∠1=∠2,∠3=∠4,∠E=90°,求证:AB∥CD.
如图,∠1=∠2,∠3=∠4,∠E=90°,求证:AB∥CD.