题目内容
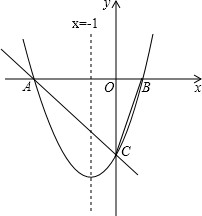 对称轴为直线x=-1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(-3,0).
对称轴为直线x=-1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(-3,0).(1)求点B的坐标.
(2)点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
考点:二次函数的最值,待定系数法求一次函数解析式,二次函数图象上点的坐标特征,抛物线与x轴的交点
专题:
分析:(1)利用二次函数对称性即可得出B点坐标;
(2)首先利用待定系数法求二次函数解析式,进而求出直线AC的解析式,再利用QD=-x-3-(x2+2x-3)进而求出最值.
(2)首先利用待定系数法求二次函数解析式,进而求出直线AC的解析式,再利用QD=-x-3-(x2+2x-3)进而求出最值.
解答:解:(1)∵点A(-3,0)与点B关于直线x=-1对称,
∴点B的坐标为(1,0).
(2)∵a=1,∴y=x2+bx+c.
∵抛物线过点(-3,0),且对称轴为直线x=-1,
∴
∴解得:
,
∴y=x2+2x-3,
且点C的坐标为(0,-3).
设直线AC的解析式为y=mx+n,
则
,
解得:
,
∴y=-x-3
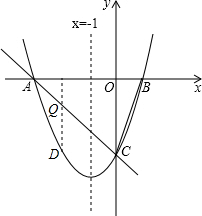
如图,设点Q的坐标为(x.y),-3≤x≤0.
则有QD=-x-3-(x2+2x-3)=-x2-3x=-(x+
)2+
∵-3≤-
≤0,∴当x=-
时,QD有最大值
.
∴线段QD长度的最大值为
.
∴点B的坐标为(1,0).
(2)∵a=1,∴y=x2+bx+c.
∵抛物线过点(-3,0),且对称轴为直线x=-1,
∴
|
∴解得:
|
∴y=x2+2x-3,
且点C的坐标为(0,-3).
设直线AC的解析式为y=mx+n,
则
|
解得:
|
∴y=-x-3

如图,设点Q的坐标为(x.y),-3≤x≤0.
则有QD=-x-3-(x2+2x-3)=-x2-3x=-(x+
| 3 |
| 2 |
| 9 |
| 4 |
∵-3≤-
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
∴线段QD长度的最大值为
| 9 |
| 4 |
点评:此题主要考查了二次函数最值问题以及待定系数法求一次函数和二次函数解析式等知识,正确得出QD的解析式是解题关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼塔第2个图案需10根小木棒,…,依此规律,拼成第6个图案小木棒( )


| A、36根 | B、48根 |
| C、54根 | D、64根 |
把二次函数y=5x2的图象先向左平移3个单位,再向下平移2个单位后,所得二次函数图象的解析式是( )
| A、y=5(x+3)2-2 |
| B、y=5(x+3)2+2 |
| C、y=5(x-3)2-2 |
| D、y=5(x-3)2-2 |

 如图,分别画出点A、B、C到BC、AC、AB的垂线段,并量出点A到BC,点B到AC,点C到AB的距离.
如图,分别画出点A、B、C到BC、AC、AB的垂线段,并量出点A到BC,点B到AC,点C到AB的距离.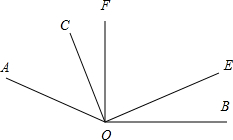 已知∠AOB=160°,∠COE=180°,OF平分∠AOE.如图,若∠COF=14°,则∠BOE=
已知∠AOB=160°,∠COE=180°,OF平分∠AOE.如图,若∠COF=14°,则∠BOE=