题目内容
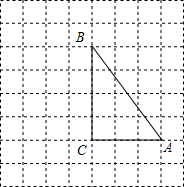 如图所示的网格中,每个小网格都是边长为1的正方形,每个小正方形的顶点叫格点,△ABC的顶点都在格点上.在AC的延长线上取一点D,D也在格点上,并连接BD.
如图所示的网格中,每个小网格都是边长为1的正方形,每个小正方形的顶点叫格点,△ABC的顶点都在格点上.在AC的延长线上取一点D,D也在格点上,并连接BD.(1)如果AC=CD,则△ABD是
(2)如果△ABD是以BD为底的等腰三角形,求△ABD的周长.
考点:等腰三角形的判定与性质,勾股定理
专题:网格型
分析:(1)由AC=CD,BC⊥AD,根据线段的垂直平分线得出BD=BA,因此△ABD是等腰三角形;
(2)先根据勾股定理求出AB、BD的长,即可求出周长.
(2)先根据勾股定理求出AB、BD的长,即可求出周长.
解答:解:(1)∵AC=CD,BC⊥AD,
∴BD=BA,
∴△ABD是等腰三角形;
(2)∵AB=
=5,BD为底边,如图所示:

∴AD=AB=5,
∴CD=5-3=2,
∴BD=
=2
,
∴AB+AD+BD=10+2
.
∴BD=BA,
∴△ABD是等腰三角形;
(2)∵AB=
| 32+42 |

∴AD=AB=5,
∴CD=5-3=2,
∴BD=
| 22+42 |
| 5 |
∴AB+AD+BD=10+2
| 5 |
点评:本题考查了勾股定理、线段的垂直平分线的性质以及等腰三角形的判定;证明等腰三角形和运用勾股定理是解题的关键.

练习册系列答案
相关题目
若抛物线y=ax2+bx+c的对称轴是x=-2,则
等于( )
| a |
| b |
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
 如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
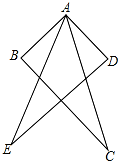 如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.
如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.

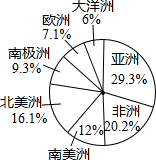 如图反映的是地球上七大洲的面积占陆地总面积的百分比,小明根据如图得出了
如图反映的是地球上七大洲的面积占陆地总面积的百分比,小明根据如图得出了