Question

15．如图1，两个不全等的等腰直角三角形OAB和等腰直角三角形OCD叠放在一起，并且有公共的直角顶点O．

（1）在图1中，你发现线段AC，BD的数量关系是相等，直线AC，BD相交成90度角．
（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．

Answer 1

分析 （1）由图可知线段AC，BD相等，且直线AC，BD相交成90°角．
（2）以上关系仍成立．延长CA交BD于点E，根据勾股定理可证得AC=BD，即可证明△AOC≌△BOD，根据两全等三角形对应角的关系，即可证明CE⊥BD．

解答 解：（1）在图1中，线段AC，BD的数量关系是相等，直线AC，BD相交成90度角；
故答案为：相等，90；
（2）（1）中结论仍成立；
证明如下：如图延长CA交BD于点E，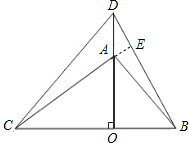
∵等腰直角三角形OAB和OCD，
∴OA=OB，OC=OD，
∵AC²=AO²+CO²，BD²=OD²+OB²，
∴AC=BD；
在△DOB与△COA中，$\left\{\begin{array}{l}{OA=OB}\\{OC=OD}\\{AC=BD}\end{array}\right.$，
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．

点评 本题主要考查了全等三角形的判定和性质，涉及到等腰直角三角形的性质、旋转的性质，熟练掌握全等三角形的判定方法是解题的关键．