题目内容
16. 如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=135°,则∠EOD=67.5°.
如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=135°,则∠EOD=67.5°.
分析 由图形可知∠DOE=∠DOC+∠EOC,然后根据角平分线的性质,可推出∠DOC=$\frac{1}{2}$∠BOC,∠EOC=$\frac{1}{2}$∠AOC,由此可推出∠DOE=$\frac{1}{2}$∠AOB,最后根据∠AOB的度数,即可求出结论.
解答 解:∵OD是∠BOC的平分线,OE是∠AOC的平分线,
∴∠DOC=$\frac{1}{2}$∠BOC,∠EOC=$\frac{1}{2}$∠AOC,
∴∠DOE=∠DOC+∠EOC=$\frac{1}{2}$∠AOB,
∵∠AOB=135°,
∴∠EOD=67.5°.
故答案为:67.5°.
点评 本题主要考查角平分线的性质,关键在于运用数形结合的思想推出∠DOE=∠DOC+∠EOC=$\frac{1}{2}$∠AOB.

练习册系列答案
相关题目
7.若等边三角形ABC内接于⊙O,点P在$\widehat{CAB}$上(P不与B、C重合),则∠BPC等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
1.一个多边形截去一个角(截线不过顶点)之后,所形成的多边形的内角和是2520°,那么原多边形的边数是( )
| A. | 19 | B. | 17 | C. | 15 | D. | 13 |

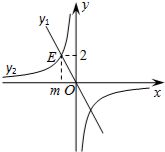 如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2).
如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2). 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 如图,一次函数y1=kx+1与二次函数y2=ax2+bx-2交于A,B两点,且A(1,0)抛物线的对称轴是x=-$\frac{3}{2}$.
如图,一次函数y1=kx+1与二次函数y2=ax2+bx-2交于A,B两点,且A(1,0)抛物线的对称轴是x=-$\frac{3}{2}$.