题目内容
7.若等边三角形ABC内接于⊙O,点P在$\widehat{CAB}$上(P不与B、C重合),则∠BPC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 根据等边三角形的性质求出∠A的度数,再根据同弧所对的圆周角相等即可求出∠BPC的度数.
解答 解:如图所示:
∵△ABC为等边三角形,
∴∠A=60°,
∴∠BPC=∠A=60°.
故选:C.
点评 本题考查了等边三角形的性质、圆周角定理;熟练掌握等边三角形的性质,熟记同弧所对的圆周角相等是解决问题的关键.

练习册系列答案
相关题目
17.若等腰三角形的有一个角为100°,则它一腰上的高与底边的夹角是( )
| A. | 50° | B. | 40° | C. | 10° | D. | 80° |
18.下列四个命题:①直径是弦;②经过三个点一定可以作圆;③正六边形是轴对称图形.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.二次函数y=kx2-2x+1的图象与x轴有两个交点,则k的取值范围是( )
| A. | k<1 | B. | k<1且k≠0 | C. | k≤1 | D. | k≤1且k≠0 |
 如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=135°,则∠EOD=67.5°.
如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=135°,则∠EOD=67.5°.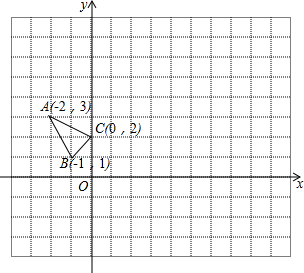 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.