题目内容
11.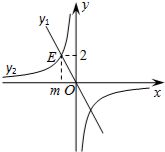 如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2).
如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2).(1)求反比例函数y2的解析式.
(2)观察图象直接写出当y1>y2时,x的取值范围.
分析 (1)设反比例函数解析式为${y_2}=\frac{k}{x}$,把E(m,2)代入y1=-2x求得m的值,然后根据待定系数法即可求得反比例函数的解析式;
(2)求出另一个交点坐标,再由函数图象即可得出结论.
解答 解:(1)设反比例函数解析式为${y_2}=\frac{k}{x}$,
∵y1=-2x过点E(m,2),
∴-2m=2,
解得m=-1,
∴E(-1,2)
∵${y_2}=\frac{k}{x}$过E(-1,2)
∴k=-2,
∴反比例函数解析式为${y_2}=-\frac{2}{x}$;
(2)解$\left\{\begin{array}{l}{y=-2x}\\{y=-\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{2}=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$,
∴另一个交点为(1,-2)
∴当x<-1或0<x<1时,y1>y2.
点评 本题考查的是反比例函数与一次函数的交点问题,熟练掌握待定系数法是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法中正确的是( )
| A. | 0没有相反数 | |
| B. | 单项式-$\frac{3{xy}^{2}}{2}$的系数是-3 | |
| C. | 任意一个数的绝对值一定是一个非负数 | |
| D. | 3.020×105有3个有效数字 |
20.下列说法正确的是( )
| A. | πx2y的系数是1 | B. | $\frac{1}{2}$xy2的次数是3 | ||
| C. | -27ab2的系数是27 | D. | $\frac{4abd}{3}$的系数是4 |
 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC. 如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=135°,则∠EOD=67.5°.
如图,∠AOB中,OD是∠BOC的平分线,OE是∠AOC的平分线,若∠AOB=135°,则∠EOD=67.5°. 如图,二次函数y=(x-h)2+k的顶点坐标为M(1,-4).
如图,二次函数y=(x-h)2+k的顶点坐标为M(1,-4).