题目内容
11.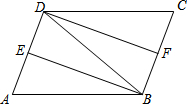 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
分析 (1)首先利用平行四边形的想得到AB=CD,∠A=∠C,再利用角平分线的性质得到∠ABE=∠CDF,利用ASA证明△ABE≌△CDF;
(2)证明∠DEB=∠BFD=∠EDF=90°.即可解决问题..
解答 (1)证明:∵四边形ABCD是平行四边形
AB=CD,∠A=∠C.
AB∥CD,∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,∠CDF=∠CDB.
∴∠ABE=∠CDF.
在△ABE和△CDF中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{AB=CD}&{\;}\\{∠ABE=∠CDF}&{\;}\end{array}\right.$
∴△ABE≌△CDF(SAS).
(2)解:四边形DFBE是矩形.理由如下:
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∵AB=DB,AB=CD,
∴DB=CD.
∵DF平分∠CDB,
∴DF⊥BC,即∠BFD=90°.
在□ABCD中,∵AD∥BC,
∴∠EDF+∠DEB=180°.
∴∠EDF=90°.
∴∠DEB=∠BFD=∠EDF=90°.
∴四边形DFBE是矩形.
点评 本题考查全等三角形的判定、平行四边形的性质、角平分线的定义、矩形的判定、等腰三角形的三线合一等知识,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
2.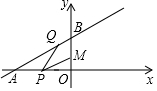 如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
 如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
20.为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则下列说法错误的是( )
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是4 | D. | 方差是1.2 |
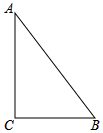 如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
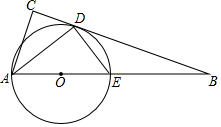 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以OA为半径的⊙O经过点D,与AB交于点E.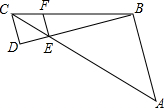 如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.
如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.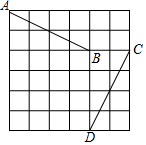 如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).
如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).