题目内容
3.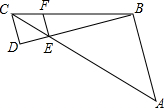 如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.
如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.
分析 先利用AB∥EF得到$\frac{CE}{EA}$=$\frac{CF}{BF}$,则可求出解得AE=12,然后利用AB∥CD,根据平行线分线段成比例定理可求出$\frac{CD}{AB}$的值.
解答 解:∵AB∥EF,
∴$\frac{CE}{EA}$=$\frac{CF}{BF}$,
∵CE=4,CF=3,AE=BC,
∴$\frac{4}{AE}$=$\frac{3}{AE-3}$,解得AE=12,
∵AB∥CD,
∴$\frac{CD}{AB}$=$\frac{CE}{AE}$=$\frac{4}{12}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.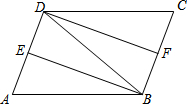 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
8.某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.商场计划用于购进这两种商品的费用不超过9000元.
(1)写出y关于x的函数关系式:
(2)该商场至少要购进多少件甲商品?销售完这些商品.商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调m元(50<m<70)出售.且限定商场最多购70件,若商场保持同种商品的售价不变,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
(1)写出y关于x的函数关系式:
(2)该商场至少要购进多少件甲商品?销售完这些商品.商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调m元(50<m<70)出售.且限定商场最多购70件,若商场保持同种商品的售价不变,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
15.下列图形:菱形、平行四边形、正方形、等边三角形、圆和线段中,既是轴对称图形又是中心对称图形的个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
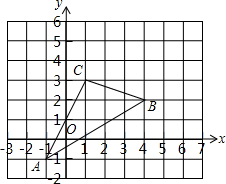 如图,△ABC在直角坐标系中,点A,B,C在格点上.
如图,△ABC在直角坐标系中,点A,B,C在格点上. 如图,已知A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,先沿射线OA的方向运动到点A,再从点A沿曲线AB运动到点B,最后沿射线BC方向运动到点C,整个运动过程中点P的运动速度保持不变,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N,设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
如图,已知A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,先沿射线OA的方向运动到点A,再从点A沿曲线AB运动到点B,最后沿射线BC方向运动到点C,整个运动过程中点P的运动速度保持不变,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N,设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )



 如图,在Rt△AOC中,∠A=30°,点O(0,0),C(1,0),点A在y轴正半轴上,以AC为一边作等腰直角△ACP,使得点P在第一象限.
如图,在Rt△AOC中,∠A=30°,点O(0,0),C(1,0),点A在y轴正半轴上,以AC为一边作等腰直角△ACP,使得点P在第一象限.