题目内容
2.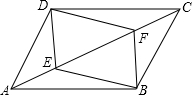 已知:如图,四边形ABCD是平行四边形,DE⊥AC,BF⊥AC,垂足分别是E、F.连结BE、DF.四边形DEBF是什么特殊的四边形?请说明理由.
已知:如图,四边形ABCD是平行四边形,DE⊥AC,BF⊥AC,垂足分别是E、F.连结BE、DF.四边形DEBF是什么特殊的四边形?请说明理由.
分析 先证出DE∥BF,再由平行四边形的性质得出CD=AB,CD∥AB,由AAS证明△CDE≌△ABF,得出DE=BF,即可得出四边形DEBF是平行四边形.
解答 解:四边形DEBF是平行四边形;理由如下:
∵DE⊥AC,BF⊥AC,
∴DE∥BF,∠DEC=∠BFA=90°,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠BAF,
在△CDE和△ABF中,
$\left\{\begin{array}{l}{∠DEC=∠BFA}&{\;}\\{∠DCE=∠BAF}&{\;}\\{CD=AB}&{\;}\end{array}\right.$,
∴△CDE≌△ABF(AAS),
∴DE=BF,
∴四边形DEBF是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.要调查我校初中7000多名学生的视力情况,下列调查方式最合适的是( )
| A. | 在我校初一年级学生中随机选取100名女生 | |
| B. | 在我校初二年级学生中随机选取100名男生 | |
| C. | 在我校初三年级学生中随机选取100名学生 | |
| D. | 在我校7000多名初中学生中随机选取100名学生 |
7.有一组按规律排列的数:1,2,4,8,16,32,…,第2012个数应是( )
| A. | 22012 | B. | 22011 | C. | 22010 | D. | 22009 |
14.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任意一点,下列说法不正确的是( )
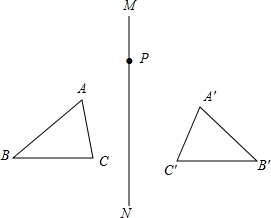

| A. | AP=A′P | B. | MN垂直平分AA′,CC′ | ||
| C. | 这两个三角形的面积相等 | D. | 直线AB、A′B的交点不一定在MN上 |
11.已知线段AC=1厘米,BC=3厘米,则线段AB的长度为( )
| A. | 4厘米 | B. | 2厘米 | C. | 2厘米或4厘米 | D. | 不能确定 |
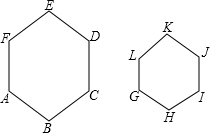 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中: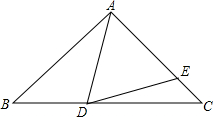 如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°.
如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°. 细图,已知∠MON=90°,在它的两边上截取OA=OB,并在它的内部任作一射线OP,作AD⊥OP于D,BE⊥OP于E.
细图,已知∠MON=90°,在它的两边上截取OA=OB,并在它的内部任作一射线OP,作AD⊥OP于D,BE⊥OP于E.