题目内容
①第二象限内一点A(x-1,x2-2),关于x轴的对称点为B,且AB=6,则x= .
②下列大写字母A,B,C,D,E,F,C,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z旋转90°和原来形状一样的有 ,旋转180°和原来形状一样的有 ,同时兼备轴对称图形和中心对称图形特点的有 .(均填出字母)
②下列大写字母A,B,C,D,E,F,C,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z旋转90°和原来形状一样的有
考点:中心对称图形,轴对称图形,关于x轴、y轴对称的点的坐标
专题:
分析:①首先表示出这个点关于x轴的对称点的坐标,其纵坐标的差为6即可求解;
②根据旋转的性质和字母特点即可解答.
②根据旋转的性质和字母特点即可解答.
解答:解:①点A(x-1,x2-2),关于x轴的对称点B的坐标为(x-1,-x2+2),
∵AB=6,
∴x2-2-(-x2+2)=6,且x-1<0
解得:x=
(不合题意,舍去),或x=-
;
②转90°和原来形状一样的有O,X;
旋转180°和原来形状一样的有H,I,N,O,S,X,Z,
同时兼备轴对称图形和中心对称图形特点的有O,H,X,I.
故答案为:-
;O,X;H,I,N,O,S,X,Z;O,H,X,I.
∵AB=6,
∴x2-2-(-x2+2)=6,且x-1<0
解得:x=
| 5 |
| 5 |
②转90°和原来形状一样的有O,X;
旋转180°和原来形状一样的有H,I,N,O,S,X,Z,
同时兼备轴对称图形和中心对称图形特点的有O,H,X,I.
故答案为:-
| 5 |
点评:本题考查了关于对称轴对称的点的坐标,中心对称图形,轴对称图形的知识,①解题的关键是根据对称点的坐标的特点列出方程;②旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
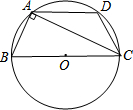 如图,梯形ABCD内接于⊙O,AD∥BC,AB=DC=AD,AB⊥AC,那么
如图,梯形ABCD内接于⊙O,AD∥BC,AB=DC=AD,AB⊥AC,那么 |
| AB |
 |
| BC |
 |
| CD |
 |
| AD |
| A、1:3:1:1 |
| B、1:2:3:1 |
| C、2:3:2:2 |
| D、2:3:3:2 |
方程ax2+bx-c=0(a>0、b>0、c>0)的两个根的符号为( )
| A、同号 | B、异号 |
| C、两根都为正 | D、不能确定 |