题目内容
7.己知一次函数y=kx+b,k从2,-3中随机取一个值,b从1,-1,-2中随机取一个值,使该一次函数的图象经过二、三、四象限,求出此时直线与坐标轴围成的三角形面积.分析 由一次函数的图象经过二、三、四象限知k<0、b<0,可得k=-3,b=-1或b=-2,分别就两种情况列出函数解析式,求出直线与坐标轴交点坐标,进而可得三角形面积.
解答 解:∵一次函数y=kx+b的图象经过二、三、四象限,
∴k=-3,b=-1或b=-2,
①当k=-3,b=-1时,直线解析式为:y=-3x-1,
∵直线y=-3x-1与x轴交点为(-$\frac{1}{3}$,0),与y轴交点为(0,-1),
∴此时直线与坐标轴围成的三角形面积为:$\frac{1}{2}$×$\frac{1}{3}$×1=$\frac{1}{6}$;
②当k=-3,b=-2时,直线解析式为:y=-3x-2,
∵直线y=-3x-1与x轴交点为(-$\frac{2}{3}$,0),与y轴交点为(0,-2),
∴此时直线与坐标轴围成的三角形面积为:$\frac{1}{2}$×$\frac{2}{3}$×2=$\frac{2}{3}$;
综上,直线与坐标轴围成的三角形面积为$\frac{1}{6}$或$\frac{2}{3}$.
点评 本题主要考查一次函数的图象与待定系数求解析式,根据函数图象所在象限求得k、b的值是解题的前提,分情况写出函数解析式并求得直线与坐标轴交点是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.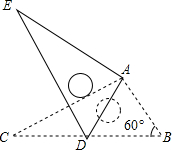 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
16.一个均匀的小立方体,它的6个面上分别标有实数5.1,$\frac{3}{4}$,$\sqrt{16}$,$\frac{π}{2}$,$\sqrt{11}$,8.$\stackrel{•}{2}0\stackrel{•}{3}$,任意掷出这个小立方体,朝上的面标有无理数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
17.近年来,中国高铁发展迅速,高铁技术不断走出国门,成为展示我国实力的新名片.预计到2015年底,中国高速铁路营运里程将达到18000公里.将18000用科学记数法表示应为( )
| A. | 18×103 | B. | 1.8×103 | C. | 1.8×104 | D. | 1.8×105 |
 如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求:
如图,在直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点按逆时针方向旋转90°得到点P1,延长OP1,到点P2,使OP2=2OP1;再将点P2绕着原点按逆时针方向旋转90°得到点P3,延长OP3到P4,使OP4=2OP3;如此继续下去.求: